Radiocarbon is produced in the atmosphere through the impact of cosmic ray neutrons on a small proportion of 14N atoms thus:



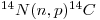
It then becomes incorporated into molecules of carbon oxides by reaction with oxygen or by exchange with stable carbon isotopes in molecules of carbon dioxide or monoxide. Molecules of 14CO2 mix relatively rapidly into the atmosphere and hydrosphere as well as living organisms to attain a constant level of concentration representing a steady state equilibrium maintained because of the continuous production of 14C and its on-going radioactive decay thus:



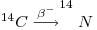
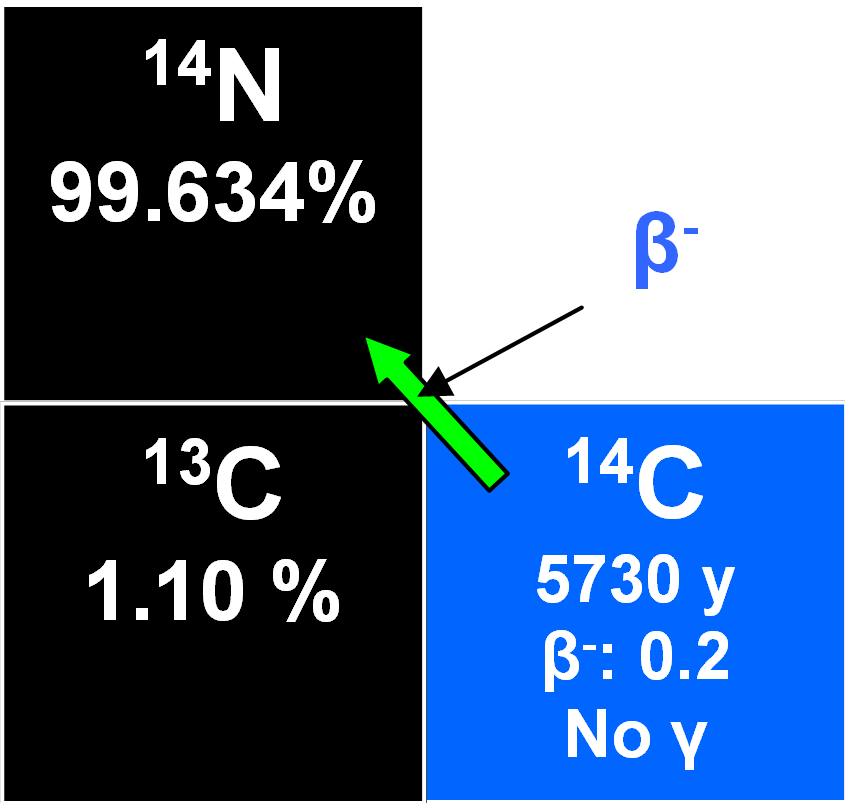
The Q-value of the above decay is only Qβ=0.156 MeV and the ground state of 14N is reached directly without γ-emission. Thus the result is a rather 'soft' β- radiation with Emax=
Qβ = 156 keV.

Radiocarbon dating can be performed on objects made from once living organisms like wood or the remnants of such organisms. The idea behind the method is that the steady state equilibrium stops between the organism and its environment as soon as the organism dies. From that moment on, the specific activity of 14C incorporated by the organism starts to decline (due to the above decay) according to the exponential law with a half-life of 5730 ± 40 y.

A multi-wire counter was used by Libby to measure the radiocarbon content in archeological artifacts. The first sample he dated was a piece of acacia wood from furniture in Pharaoh Zoser's tomb at Saqqara, Egypt. About twenty grams were used and the date determined was 2030 ± 350 years BC. The technique developed rapidly and only ten milligrams of the same sample were dated in 1992 in the new National Ocean Sciences Accelerator Mass Spectrometry (AMS) facility at Woods Hole Oceanographic Institution and gave an age of 4115 ± 34 years.

Conversion of Radiocarbon Years to Calendar Years

To do this requires corrections accounting for fluctuations of radiocarbon content in atmospheric carbon dioxide in the past. These are based on measurements of radiocarbon concentrations in a series of tree rings dated using dendrochronological techniques. The tree ring calibrated age for the modern 14C AMS equipment analysis of the Zoser wood gives two solutions with a 95% degree of confidence: 2877 to 2800 BC and 2780 to 2580 BC. This is in accord with archeological estimates. However, a marked step in the calibration curve during Zoser's reign precludes a high precision calibrated age estimate for this particular material.

The radioactive decay of radiocarbon in plant or animal tissues originally in equilibrium with atmospheric or hydrospheric 14CO2 molecules. Exchange ceases after the deaths of the organism involved. The radioactivity diminishes as a function of time (half-life of 14C is 5730 ± 40 years). When the residual radiocarbon activity is measured, the age of the sample is obtainable from this graph.

Atmospheric Radiocarbon in the Past

There have been systematic variations in the radiocarbon content of the atmosphere in the past which cause inaccuracies where dating is concerned. One reason for such variations is that the rate of formation by the (n,p) reaction shown by Eq. (20) depends mostly on the density of the cosmic-ray-produced neutron flux (see Eq. (68) in Chapter 5, Volume I) which increases with altitude to attain a maximum between 12 000 and 15 000 meters above the surface of the Earth. Also, the flux is greater by a factor of four in the polar regions. Consequently, the rate of production of radiocarbon there should mean that living tissues in that rcgion ought to have more radiocarbon in them than those at the equator. However, it has been shown that specific 14C activity may be independent of location probably because of rapid mixing in the upper atmosphere, a process believed to last less than two years. The effect of this may well tend to produce uniformity at the surface of the Earth. In addition, the neutron flux will vary as the intensity of the solar proton flux does, so that the 14C content of the atmosphere doubtless varied with time in conjunction with alternating solar activity. Additionally, the cosmic ray flux may be modified by changes in the Earth's magnetic field during the past 40 000 years or so, although data have been published implying that the initial radiocarbon in a set of archeologically dated samples was compatible with present day values (Arnold and Libby 1949).

Radiocarbon in Dead Animals and Plants

The radioactivity of a carbon sample from a plant or animal tissue which died t years ago is given by A = Aoe-λt, where A is the specific activity now and A is the specific activity of 14C in the same sample when death occurred. A value for the estimated specific activity of 14C was 226 ± 1.2 Bq/kg and the half-life, T1/2, was given as 5730 ± 40 years with a decay constant of 1.209 •10-4. A 'dead' sample containing carbon can be considered no longer in equilibrium with the 14C of the atmosphere.

From the exponential law of decay applied to (specific) activities we get:

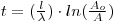
which, substituting the value of λ, gives:



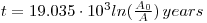
The initial activity is a known constant through the past 70 000 years independent of passing time and with a value independent of geographical location and the species of dead plant or animal from which the relevant tissues are taken. It is assumed that the sample to be dated was not contaminated by modern radiocarbon and that its observed activity is unaffected by radioactive impurities. Research has shown that the initial 14C activity of modern plant and animal tissues is constant to a first approximation and also that the radiocarbon activity in archeological materials of known age is measurable with sufficient precision to provide radiocarbon dates that agree satisfactorily with the known historical ages.

Materials suitable for radiocarbon dating include charcoal, peat, wood, grains and seeds, ivory, burnt bones, collagen, cloth, inorganic and organic carbon in shells, lake marls, lake and deep-sea sediments, pottery and iron. Amounts needed for analysis vary from about 25 grams for wood to 5 000 grams for iron. To measure the radiocarbon contents, liquid scintillation has been used and is adequate for dates < 30 000 years old. Ultra-sensitive high voltage tandem mass spectrometers offer direct counting of 14C ions, but the technique is expensive.

The De Vries Effect

It has been shown that the radiocarbon content of the atmosphere varied systematically in the past so that the radiocarbon activity around 1500 and 1700 was approximately 2% higher than it was during the nineteenth century. This phenomenon has been termed the De Vries effect and another such effect (called the Suess effect) has been observed in twentieth century activity and is ascribed to the introduction of 'dead' CO2 into the atmosphere through the combustion of fossil fuels after the start of the Industrial Revolution (De Vries 1958).

Bomb, Reactor and Accelerator Radiocarbon in the Environment

Larger effects came from atmospheric thermonuclear explosions then and later by the operation of nuclear reactor and particle accelerators. Bomb-produced radiocarbon is detectable in the oceans and also in the biosphere. To narrow uncertainty of estimates of fossil fuel anthropogenic carbon dioxide uptake by the oceans is important in quantifying the contemporary carbon budget. Using ocean general circulation models (OGCM) may be the best way of tackling this problem, but first the model has to be calibrated with the distribution of bomb-produced radiocarbon in the ocean. Natural, i.e. cosmic ray-produced, radiocarbon is most sensitive to processes operating over century time-scales, whereas anthropogenic (i.e., bomb testing-produced) radiocarbon is most sensitive to processes operating over ten year periods. If the bomb-produced radiocarbon is not separated from the natural radiocarbon, it will not be possible to determine whether the disagreements between model and observation reflect the deficiencies in the model's simulation of the steady state distribution of natural radiocarbon or in its simulation of the distribution of the bomb radiocarbon transient. Therefore, the separation of bomb-produced radiocarbon from the natural radiocarbon in the overall radiocarbon measurements is essential if radiocarbon distribution is to be used to constrain the ocean models.

Separating Bomb-Produced 14C from Natural Radiocarbon

A method of achieving such a separation has been developed. It involves the strong correlation between natural radiocarbon and dissolved silica. For global coverage, radiocarbon measurements made on samples collected during the Geochemical Ocean Sections Study (GEOSECS) in 1972-1978 were analyzed for bomb radiocarbon inventory in the ocean. Later measurements made in the Atlantic Ocean during Transient Tracers in the Ocean (TTO) in the early 1980's and South Atlantic Ventilation Experiment (SAVE) in the late 1980's were also analyzed for temporal variations in bomb radiocarbon inventory. Recent radiocarbon measurements on the NOAA/OACES 1993 cruise in the Atlantic have also been analyzed for bomb radiocarbon inventory. In the Pacific Ocean, radiocarbon measurements from samples collected in the WOCE program are gradually becoming available for bomb radiocarbon inventory analysis. Continuing efforts in analyzing WOCE data have been proposed.

Comparison of results between GEOSECS and TTO/SAVE shows that the bomb radiocarbon inventory has increased by 36% for the region north of 10° N, by 69% for the equatorial region and by 71 % for the region south of 10° S. These data reflect the radiocarbon uptake for the Atlantic Ocean between 1973 (GEOSECS) and 1985 (TTO/SAVE). As well as global bomb radiocarbon distribution, this information provides crucial constraints for the carbon cycle in the ocean. Preliminary results from CGC-91, one of the WOCE cruises, show that the observed increase in bomb radiocarbon inventory from 1974 to 1991 in the northern Pacific Ocean is consistent with the first-order prediction from a box-diffusion ocean model.

Variation of Bomb Radiocarbon in the Oceans

Variation of bomb radiocarbon in oceans has been applied to the analysis of banded corals and so to lower latitudes. A shell-derived chronological history of bomb 14C on Georges Bank and its Labrador Sea implications offered high latitude data resulting from the analysis of a fifty-four year old mollusk (age assessed from annual growth bands) using accelerator mass spectrometry. This gave a time history from 1939 to 1990 and so widened the scope of such investigations. Other significant information came from the southern Great Barrier Reef in Australia (Druffel and Griffin 1993). Radiocarbon and stable isotope (Δ18O and Δ13C) data for biannual samples were obtained from a 323 years banded coral series collected from the region. The high precision Δ14C record showed variations on an inter-annual time-scale that were especially large from 1680 to 1730. This may have nothing to do with atmospheric changes, but perhaps involved in vertical mixing and large-scale advective changes of source waters to the western Coral Sea. Low values from 1935 to 1875 may relate to El Nino/Southern Oscillation (ENSO) events in the eastern tropical Pacific. But these cannot explain all the variations, especially those from 1875 to 1920 characterized by high Δ14C values. The time interval 1635 to 1795 appears to embody a six-year periodicity, a coherency later lost. It may be inferred that secular changes take place in the nature and properties of the ENSO as manifested in the south-western Pacific. Interestingly, no trace of the Suess effect was found from the coral record.

Dendrochronology and Radiocarbon

Further to previous remarks regarding Zoser's tomb and the converting of radiocarbon years to calendar ones, analyzing old trees facilitated investigation of the secular variations of the radiocarbon content of the atmosphere. Such trees can be dated using tree rings, annual accretions of woody tissue to the circumferences of their trunks.

Layers deposited earlier cannot receive radiocarbon from the atmosphere anymore so that their radiocarbon contents decrease by radioactive decay. Two tree species that have been used are Pinus aristato (bristlewood pine) and Sequoia gigantea (sequoia).

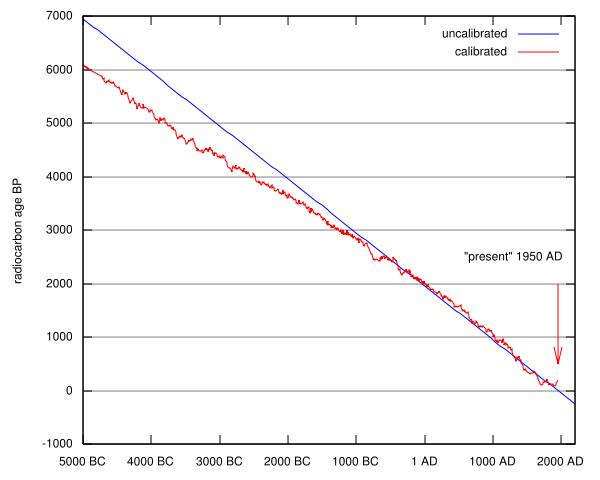
Combining dendrochronology with isotopic investigations enables age-corrected deviations of the radiocarbon contents of such trees to be used in calculating corrections applicable to conventional radiocarbon dates. The drawback is that the technique is valid only back about 12000 years into the past. However, examination of varve chronologies of sediments deposited in glacial lakes extends the approach further back. The researches imply that the radiocarbon content of the atmosphere varied by about ± 10% of the nineteenth century value.

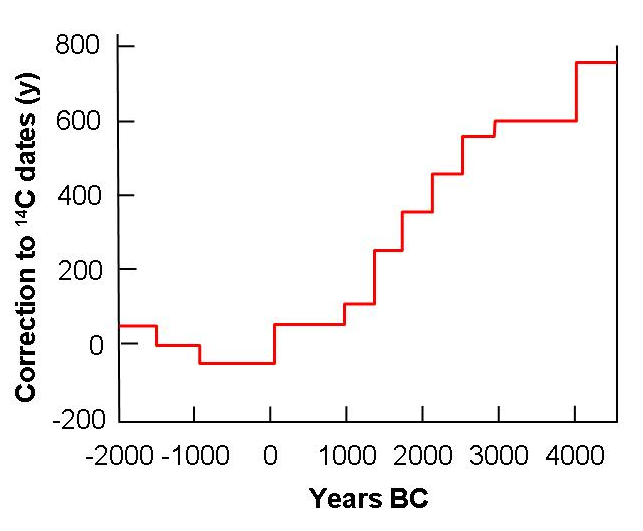The graph gives the corrections which have to be added to radiocarbon dates so as to bring them into agreement with tree ring dates based on 143 analyses of the wood of bristlecone pine (Pinus aristato) and sequoia (Sequoia gigantea) which gave dendrochronological dates.

Radiocarbon and Dating of Groundwaters

Radiocarbon is important for dating groundwaters on the basis that the soil-zone carbon dioxide is of biogenic origin resulting from the respiration of plant roots and also from the decay of plants. So, indirectly, it contains radiocarbon from the atmosphere. The actual content of the radioisotope decays steadily since the gas is no longer in contact with the atmosphere and the fraction of the original content remaining is a measure of the time elapsed since this happened through infiltration. The time since this occurred, t, is given by: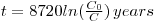



where 8270 is the mean life of radiocarbon in years, C0 is the initial concentration of the radiocarbon and C is the concentration recorded in the sample.

Since radiocarbon is measured relative to the total carbon content of the sample, the origin of the stable carbon present must be examined as well. Not all of it is similar in origin to the atmospheric radiocarbon since infiltrating water contains carbon dioxide dissolved out of the soil zone which dissolves carbonate minerals in the soil. However, water from limestone contains no radiocarbon and therefore that which reaches the water table contains dissolved carbon in the chemical forms H2CO3, HCO3- and CO32- with a radiocarbon content lower than that occurring in the soil (biogenic) carbon dioxide. The evaluation of the dilution of soil carbon dioxide originally containing 100% modem radiocarbon with radiocarbon-free ('dead') carbonate in order to estimate the initial radiocarbon concentration in recharge water reaching the water table is one of the most difficult problems of radiocarbon age determination.

An interesting study of the frequency distribution of radiocarbon ages in groundwater samples collected in the Sahara has appeared (lAEA 2002). It has been known for at least a century that large reserves of groundwater lie beneath the Sahara, the largest desert in the world. Radiocarbon dating made it possible to estimate the age of these groundwater. From a graph based on three hundred and fifty samples collected in Algeria, Libya, Egypt and the Southern Sahara, it was shown that aquifers in Northern Africa were recharged mainly during the pluvial periods of the Holocene and during the inter-stadials of the last glacial period. A well-marked minimum in the distribution curve ranging from approximately twelve to twenty thousand years B.P. reflects the time interval of maximum aridity in Northern Africa. This estimate of the groundwater age is critical in exploiting this groundwater resource, all the more so since absence of tritium and low concentrations of radiocarbon strongly imply that the aquifer in question is not being replenished at present.

Fraction of Carbon Isotopes in Nature

Fractionation of the carbon isotopes in nature entails small systematic errors in radiocarbon dates that can be eliminated when the isotopic composition of stable carbon to be dated can be assessed using a mass spectrometer. The value is expressed as δ13C ‰. Such fractionation during photosynthesis alters the abundances of the stable isotopes 12C and 13C from those prevailing in the atmosphere and plants usually become enriched in 12C and depleted both in 13C and 14C.