In this exercise you are going to make a calibration source of uranium. You will use this source to calibrate and get some experience with using a gas-filled detector. You will then use the source to investigate uncertainty in radioactive measurements.
Your supervisor will demonstrate and explain the various equipment you are going to use. Never just "try it out" but ensure that you know exactly what to do and how before you do any operations with radioactive material.
Before you can start in the lab you must calculate the exact amount of uranium needed for calibration source. Therefore you should answer the following questions before you arrive at the lab. Write the answers down in your laboratory journal and ask your supervisor to check before you start any work in the lab.
Question 1:
Draw the disintegration schematic of the uranium series from 238U to 230Th. Write down the half-lives and the type of disintegration, including the energy of emitted particles.
Question 2:
Assume that the sample of uranium that you have is one year old. (The uranium is chemically separated from the other elements). Why is 234Th, 234Pa and 234U in equilibrium with 238U, while 230Th is not?
Question 3:
Show that the amount of 238U and 234U is in agreement with the equilibrium definition λ1N1=λ4N4. (Assume the abundance of the two isotopes is equal to the abundance in natural uranium.)
Question 4:
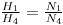Here H1 symbolizes the atomic abundance of a 238U and H4 symbolize the atomic abundance of 234U . Compare this with
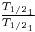Does this agree with the claim that the two isotopes are in equilibrium?Question 5:
What is the mass of UO3 that must be weighted in to get the right amount of the radioactive calibration source you are going to make?. Assume that the the counting speed R should be equal to 100 cps and that the counting efficiency is ε = 15%. Your counter will measure high-energy betas (the disintegration yielding low-energy betas will not be measured since we shield the source with 7 layers of tape - low-energy betas will not get through).
Background
Note down the values from the background measurement. The longer the measurement the better. Preferably it should be started the day before.Counting number:
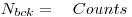
Counting Time:
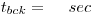
Standard deviation:
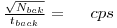
Counting Efficiency
Do a one minute count on every shelf that is in the detector. Use these measurements to calculate the counting -efficiency of the GM-detector in %. The activity of the sample can be calculated from the amount of UO3 used.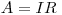
where A is the true activity I is the efficiency of the detector and R is the observed counting number.
| Shelf Number |
Counts per minute |
Calculated efficiency from amount of uranium |
| 1 |
||
| 2 |
||
| 3 |
||
| 4 |
||
| 5 |
Twenty measurements with constant distance from the source
Do twenty measurements lasting for one minute. Keep the source fixed to one position. Calculate the standard deviation and complete the table| measurement number |
NP |
NP-Naverage |
(NP-Naverage)2 |
| 1 |
|||
| 2 |
|||
| 3 |
|||
| 4 |
|||
| 5 |
|||
| 6 |
|||
| 7 |
|||
| 8 |
|||
| 9 |
|||
| 10 |
|||
| 11 |
|||
| 12 |
|||
| 13 |
|||
| 14 |
|||
| 15 |
|||
| 16 |
|||
| 17 |
|||
| 18 |
|||
| 19 |
|||
| 20 |
|||
| 21 |
|||
| 22 |
|||
| 23 |
|||