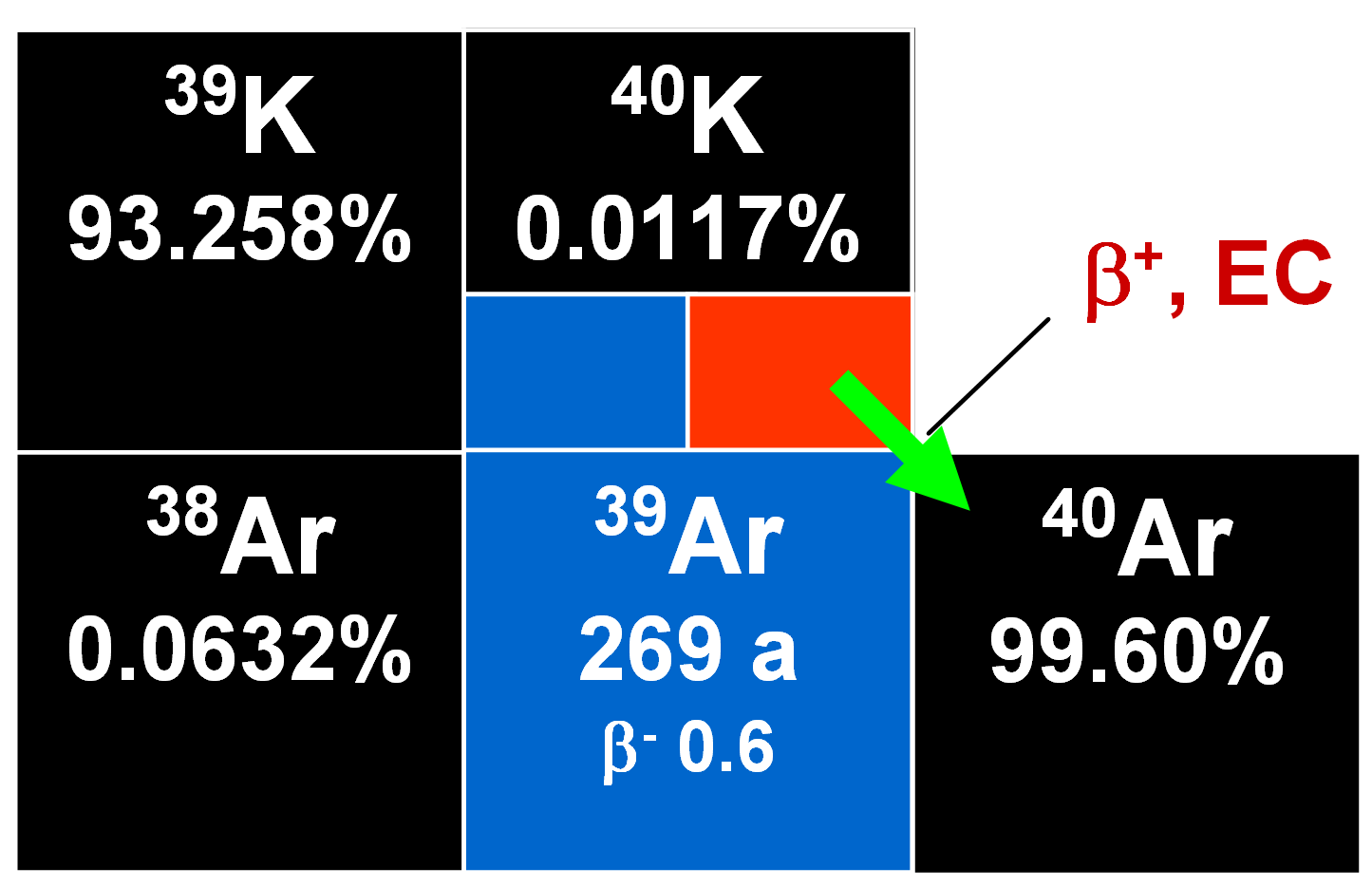
The argon/argon method is partly based on the formation of 39Ar by irradiation of potassium-bearing samples using both thermal and fast neutrons in a nuclear reactor. The relevant reaction is:

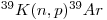eqn 1

39Ar is radioactive, decaying by beta emission with a half-life of 269 years, a fact that makes it stable in terms of the relatively insignificant analytical times involved in research. A counting technique for the assessment of 39Ar was superseded in the middle 1960' s by mass-spectrometric determination of the [40Ar/39Ar] ratio. It is assumed that all 40Ar in the irradiated sample is either radiogenic or atmospheric in origin and that 39Ar is produced by the (n,p) reaction as shown by Eq. (1).

During the irradiation process, reactions occur that involve potassium, calcium and chlorine, but the only one of interest is that cited above. The number of radiogenic 40Ar* atoms present in a sample due to the radioactive decay of 40K during its geological history is given by:

eqn 2

where λEC is the decay constant of 40K for electron capture, λ is the total decay constant of 40K (including β- decay), λ = λEC + λβ, and t is the age.

After the neutron irradiation process, the [40Ar/39Ar] ratio can be determined and compared with the [40Ar/39Ar]fm ratio of a flux monitor the age of which is known. Various mineral concentrates can be used as flux monitors. It is assumed that all 40Ar in the irradiated sample derives either from a radiogenic or an atmospheric origin, 36Ar is purely atmospheric, and also that all 39Ar is produced by the (n,p) reaction shown in Eq. (1).

Several corrections have to be introduced, especially as regards younger samples (~ 106 years) and those having [K/Ca] < 1.0. Particularly important are interfering reactions involving calcium isotopes. For instance, 36Ar is produced by the reaction:

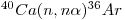eqn 3

and removed by the reaction:

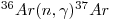eqn 3

Also, an atmospheric 40Ar correction is relevant both to conventional potassium/argon and 40Ar/39Ar dating methods. The assumption is made that 36Ar is of atmospheric origin and that the ratio [40Ar/36Ar] in the atmosphere is 295.5. However, both 40Ar and 36Ar may become incorporated into minerals when they crystallize so that the [40Ar/36Ar] ratio of this argon may differ significantly from that of atmospheric argon today. Consequently, the observed quantity of argon-36 in a mineral or rock may not allow an accurate correction to be made for the presence of non-radiogenic 40Ar. Where the [40Ar/36Ar] ratio of the inherited argon exceeds 295.5, an apparent excess of radiogenic argon will result. But if the value of this ratio is below 295.5, an apparent deficiency of radiogenic argon will result. This latter might mistakenly be attributed to a partial loss of 40Ar.

It is possible to calculate a date from the [40Ar/39Ar] ratio of a sample that has been irradiated by neutrons. A set of such dates can be obtained for the sample if argon is liberated from it in steps following temperature increases. If the sample was a closed system for both argon and potassium since it first cooled, the dates obtained from each step should be constant. However, if some loss of radiogenic argon occurred and took place in regard to some, but not all, crystallographic sites, the [40Ar/39Ar] ratios of the gas released at different temperatures will vary and a range of dates will result. From this, the time elapsed since initial cooling can be derived.

It has been indicated that the 40Ar/39Ar approach has several advantages over the potassium/argon method. Perhaps the greatest is that only ratios of argon isotopes have to be measured in order to calculate an age rather than absolute quantities. Hence it is not necessary to extract all radiogenic argon from a mineral to derive an accurate age. Thus one avoids a problem inherent in the potassium/argon dating: Sometimes it may be difficult to extract all argon from minerals, - even from mineral melts under vacuum.