Back to Measurement, Uncertainty and Detection Limits

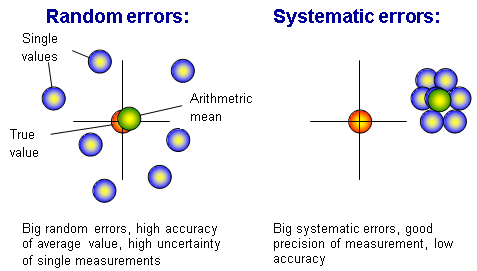
Accuracy and Precision


The two terms are defined in the fig. below:
Random-systematic-errors.png

The Measurement Process

Often the measurand Y is not measured directly, but instead an estimate is calculated from the measured values of other input quantities X1….Xn.
These input quantities have a known mathematical relationship to the measurand. In general:

Y=f(X_1,X_2,X_3....)
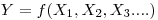
Example:
Measurement of activity concentration Ac (Bq/g or Bq/L) in a sample may include the gross counting rate (Rs), blank or background counting rate (Rb), counting efficiency () including geometry effect and radiation branching ratio and, test sample weight (w):

Y=A_c=\frac{R_s-R_b}{\epsilon\cdot W}


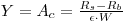
Measurement Uncertainty


When the measurement is performed, a value xi is estimated for Xi and an estimated value y of the measurand is calculated using the relationship
Y=f(X_1,X_2,X_3....)
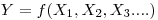
Since there is an uncertainty in each input estimate xi, there is also an uncertainty in the output estimate y.
The uncertainty of xi is expressed by an estimated standard deviation (standard uncertainty) denoted u(xi). It may also be expressed in the form of an estimated variance denoted u2(xi).
The ratio u(xi)/|xi| is called the relative standard uncertainty of xi.