Table of Contents
Hence, the residence time of uranium in oceans is longer by orders of magnitude than that of thorium, namely ~ 0.5 million years compared to about 300 years. Most 230Th in seawater is formed right there from dissolved 234U, but about a quarter is thought to come from river inputs. The preferential removal of 230Th from seawater separates the radionuclide from its parent and produces an excess of unsupported 230Th in the sediments. This causes activity that falls off with time, this assuming that both locally formed and river-derived components are altogether removed from seawater.
A sample of sediment from a given depth below the water/sediment interface can be dated from its (230Th/232Th) activity ratio if this has stayed constant for at least several hundred thousand years in the water body next to the sediment in any given ocean basin and also if there was no migration of the isotopes in the sediments. In addition, their chemical speciation must have been the same in seawater with no isotopic fractionation between this and the mineral phases involving thorium in the sediment. Furthermore, the 230Th and thorium found in detrital mineral particles must be excluded from the analysis. Assuming that the contribution made by uranium-supported 230Th is negligible, the activity of a sample given as an activity ratio may be related to its age thus:
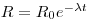
where R is the 230Th /thorium activity ratio of the leachable fraction of sediment obtained at a given depth below the top of a core, R0 is the same ratio for the newly deposited sediment, λ is the decay constant of ionium and t is the time elapsed since deposition occurred. R is measured and, if R0 is known, then:
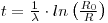
This approach has been used to determine the rate of sedimentation in oceans and this varies greatly due to factors such as the quantity of debris introduced by rivers, the rates of melting of icebergs and the number of particles transported through and deposited by the atmosphere. The ionium/thorium method covers a range from less than 0.5 mm per thousand years to 50 mm per thousand years on a carbonate and opal-free basis, the lower figures applying to the South Pacific and the higher ones to the Atlantic. This is paralleled by variation in 230Th /232Th) activity ratios at the surfaces from which it has been inferred that there is a greater input of 232Th in the Atlantic. This may be due to the many large rivers that enter it. But an excess 230Th method may be applicable for separating ocean sediments into fractions which form isochrons of which the intercepts decrease with depth in the core. However, the slope of the isochron in young samples was found not to be zero, as expected, but rather showed disequilibrium among the thorium isotopes in the sediment (Bernat and Allegre 1974).
230Th/231Pa
Protactinium is a radioactive element with over twenty isotopes of which the one of interest is 231Pa with a half-life of 32 480 years and a corresponding decay constant of 2.134•10-5 y-1. It is a daughter of 231Th in the 235U radioactive decay series. In oceans, its geochemical properties resemble those of thorium since the isotopes are removed from seawater either by adsorption on mineral grains or by incorporation into authigenic minerals. Hence, sediments deposited in oceans may contain not only excess unsupported 230Th, but also unsupported 231Pa. If both are removed from seawater equally efficiently, their activity ratios will change with time in a manner controlled by their decay constants.
The ratios of the activities of the unsupported 231Th and 231Pa increase with depth in cores and, if the sediment is deposited at a uniform rate, then the following expression below may be applicable:
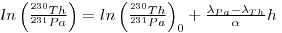
where h is the depth in the core and α = h/t is the constant rate of sedimentation.
This is a straight-line equation in coordinates of h and ln(230Th/231Pa). Its slope will be inversely proportional to the rate of sedimentation and its intercept equals the logarithm of the initial value of the activity ratio of the relevant unsupported 230Th and 231Pa in the sediment, i.e. ln(230Th/231Pa)0. The approach has been used to determine α for a core from the Arctic Ocean and a value of 0.2 cm per thousand years was derived (Baxter et al. 1981).
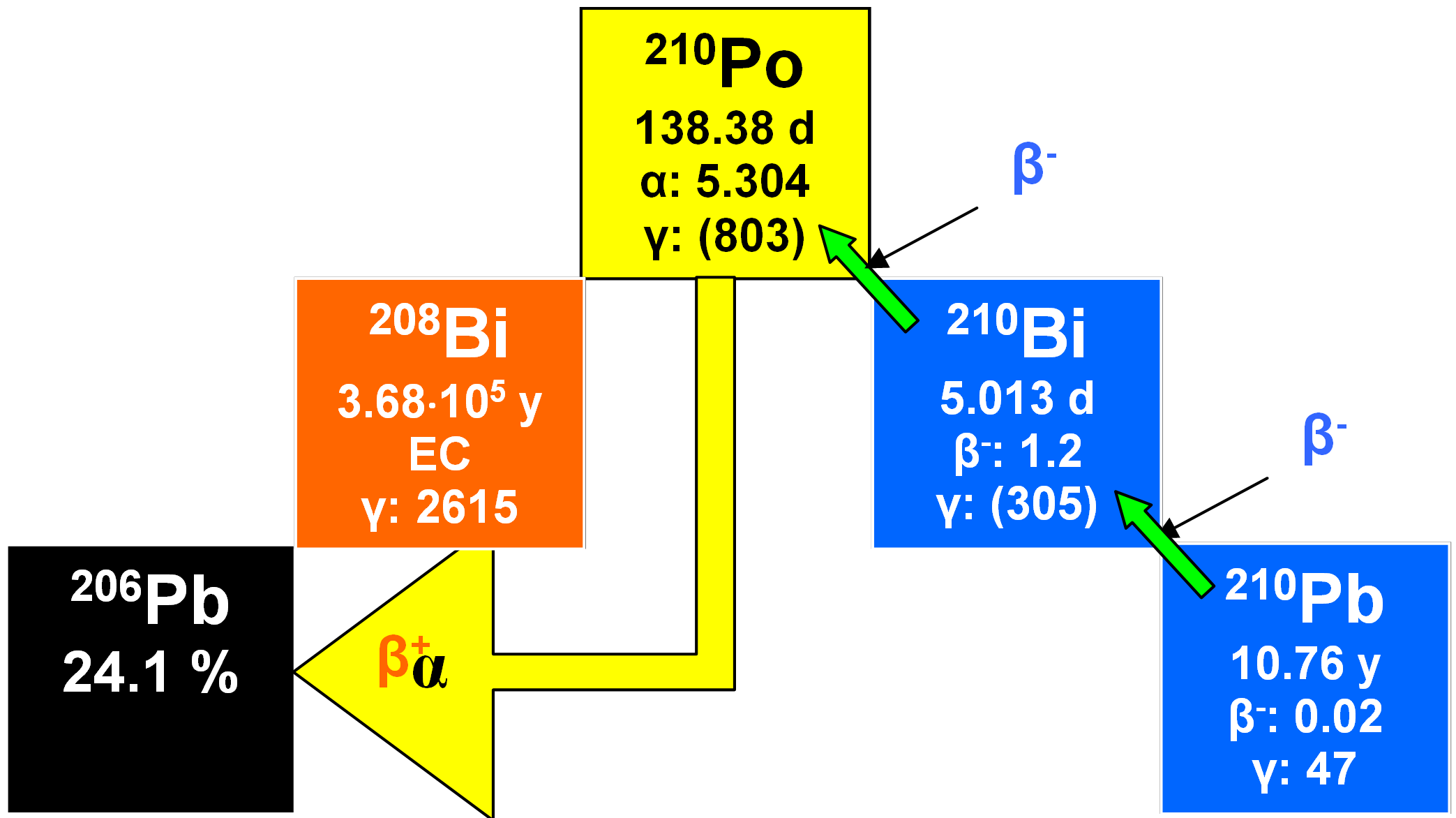
210Pb
In the uranium series, a daughter of 238U (namely 222Rn) enters the atmosphere and later decays through several short-lived daughters to 210Pb with a half-life of 22.3 years (see also Section 14 on the polonium/lead method). This radionuclide is removed by precipitation with a residence time of about ten days. Later this may deposit on snow and ice in glaciers as well as in lakes and coastal regions. The activity of unsupported 210Pb diminished thereafter as a function of time at a rate determined by its half-life. 210Pb can be used to date materials containing it. Owing to the short half-life of 210Pb, the dating range is only a few hundred years. The method has been used for measuring the rates of deposition of snow in Greenland and Antarctica as well as on Alpine glaciers. Lake sediments have been dated using the method, for instance some from Loch Lomond in Scotland.
In addition to the unsupported (excess) 210Pb of atmospheric origin, this radionuclide is also found unsupported by its primary parent 238U but supported by excess 226Ra in sediment minerals, i.e. at equal activity to the latter through in situ production from 226Ra. This component is controlled by sediment mineralogy and so gives no information about time-scales. The unsupported 210Pb is quantified by subtracting the measured activity of supported 210Pb from the total 210Pb inventory at each depth in a core. 222Rn activity is measured and the total inventory assessed by analysis of 210Pb decay products 210Bi or 210Po. In all cases, secular equilibrium is assumed for the parent/daughter pairs. Thus, the conventional dating method is indirect and specialized, involving nuclear counting equipment and radiochemical expertise. A more practical alternative is offered by a particle track approach which depends on counting radiation damage tracks produced in selected plastic films by both alpha particles and fission products emitted from essentially in processed dried sediment. Supported 210Pb is measured indirectly by 235U analysis. Because the [235U/238U] ratio does not vary significantly in nature, the 238U content of a sample can be calculated and secular equilibrium with 210Pb again invoked. The supported 210Pb profile is then subtracted from the total alpha record and the assumption made that the resultant excess alpha-plot is dominated by the decay of unsupported 210Pb (or 210Po). Using this method depends on an idealized non¬migratory behavior for another uranium series alpha-emitters and also on total constancy with depth of 232Th and its decay products.
Snow, Ice and Volcanoes
As regards snow and ice chronology, the time elapsed since a sample of snow deposited at a depth h from the surface can be calculated from the activity of 210Pb if the initial activity of this radioisotope has remained constant so that:
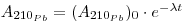
where the first term expresses the activity per unit mass of sample at depth h, (A210Pb)0 is the specific activity at the surface (where h = 0), A. is the decay constant of 210Pb (3.11 •10-2 y-1) and t is the age of the snow sample. From this the following may be derived:
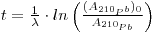
Excess 210Pb unsupported by 238U occurs in volcanic rocks and arises partly from the radioactive decay of excess 226Ra (half-life 1602 years). A sample from Mount Vesuvius showed enrichment in 226Ra and so in 210Pb also. There is a high 210Pb activity in the mineral cotunnite (PbCl2) that occurs as a sublimate in fumaroles around the volcano and its lead probably comes from the volcanization of basalts. 210Pb activity in volcanic rocks increases through the radioactive decay of excess 226Ra so that deviations in the (210Pb/238U) activity ratios cannot just be ascribed to elemental fractionation effects in the magma. In the oceans, 210Pb distribution was examined through the GEOSECS Program, particularly in the Pacific. Oceanic boundaries were envisaged as potential sinks for reactive metals in seawater. The 210Pb deficiency relative to its ancestral 226Ra seemed to increase from oceanic interiors towards continental edges and sea floors where it is more intensively scavenged. Within about one hundred meters of the latter, a large amount of excess 222Rn relative to 226Ra has been recorded and attributed to supply by sediments through pore water diffusion. This 222Rn decays to 210Pb and so its effects on the distribution of the latter is manifested. However, some vertical profiles in the deep western North Pacific showed no significant variations with depth despite this excess of 222Rn. And the apparent box model residence time that is based on (210Pb/222Rn) activity ratios decreases from ~ 100 years in oceanic interiors to about ten years near the bottom. The 210Pb data are explicable using a vertical-mixing and first order scavenging model without enhanced scavenging near the sediment/water interface. This shows that the bottom excess 222Rn can scarcely influence 210Pb in the water and also that the short residence time mentioned may be an artifact not reflecting the chemical reactivity of lead. It may be inferred that the deficiency of 210Pb through scavenging is best estimated using 226Ra and not 222Rn. One caveat - the 210Pb scavenging at the sediment/water interface inferred from the oceanic distribution of this radioisotope-appears difficult to detect from bottom 210Pb profile measurements.
230Th, 234U, 238U
Practically no thorium, but substantial amounts or uranium are contained in calcium carbonates deposited in saline lakes and also in the oceans where they sometimes reach 5 ppm. Hence, there is almost no initial 230Th activity in newly deposited carbonates, but, due to the radioactive decay of 234U, the activity of 230Th increases with time. Consideration of this lead to the setting up of a method which has been used to date corals, for instance those from the three lowest terraces in Barbados, an island apparently emerging from the sea at a uniform rate (Broecker 1963). Data from the 230Th/234U) activity ratios of coral samples gave dates of 122 000, 103 000 and 82 000 years. These coincide with predicted times of elevated summer radiation at 45° N latitude (Milankovitch 1920). In age determinations, it is necessary that initial activity ratios (230Th/234U)0 are close to zero, also the sample must have been a closed system as regards uranium and intermediates between 238U and 230Th. In addition, the initial activity ratios (234U/238U)0 must be known.
It is possible to relate the activity of 230Th to that of its immediate parent, 234U, since, if the 234U is in secular equilibrium with 238U, then the (230Th/234U) activity ratio is related to time, t, as follows:
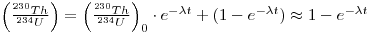
where A. is the decay constant of 230Th. Note that this equation does not take into account the possible presence of excess 234U. This, however, may not make much difference.
The 234U, 238U Geochronometer
Attainment of secular equilibrium in radioactive decay series starting with 238U, 235U and 232Th depends on that none of relevant daughters are leaving or entering the systems concerned. Once this equilibrium is established, the decay rates of the daughters in any particular system equal that of the parent:
λ1N1=λ2N2=λ3N3=...= λnNn
where λ1N1 is the activity of the parent and the other terms represent those of the daughters. Under secular equilibrium conditions, the ratio between the decay rate of any daughter and its parent is equal to one. The production of 234U from its parent proceeds as follows below:
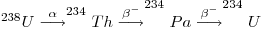
so that, where secular equilibrium exists, the rate of decay (i.e. the activity) of 234U in an uranium-bearing mineral equals that of 238U and the activity ratio (234U/238U) = 1. However, investigations from groundwater samples showed that such secular equilibrium does not exist there and was also absent from minerals deposited from the said groundwater (Thurber 1962). In fact, the value of the ratio usually exceeds unity because the 234U is enriched by such processes as the radioactive decay of its parent dissolved in groundwater. The alpha decay of the parent, namely, damages the crystal lattice and permits the daughter to migrate through micro-capillaries in the mineral and oxidize to form uranyl ions which dissolve in water and remove it into an aqueous phase. 238U occurs in stable lattice positions. 234Th can be rejected from grain surfaces through recoil caused by alpha emission then it decays to 234U through the short-lived 234Pa. Generally activity ratios (234U/238U) both in surface and groundwater as well as in secondary minerals containing uranium on continents usually exceed unity and can reach values as high as ten. But the activity ratios of primary uranium minerals in chemically weathered rocks may be less than unity through the preferential removal of 234U.
If uranium occurs in solution in ground waters, it may enter oceans and become isotopically homogenized, the relevant activity ratio (234U/238U) having a narrow spread of values with a mean around 1.15. The element uranium can be removed from oceans by incorporation into authigenic minerals such as calcium carbonate, also by adsorption on grain surfaces under reducing conditions. Once uranium has become isolated from seawater, 234U decays to 230Th until the activity ratio (234U/238U) approaches an equilibrium value. However, this is not useful as a dating method because of the possibility that 234U migrated after deposition. Nevertheless, the radioactive decay of excess 234U and the growth of its daughter 230Th have been used for dating or marine and non-marine carbonates of Pleistocene age.
The geochronometer involves determination of γo, the initial (234U/238U)o activity ratio and it has been applied to dating the calcium carbonate of biogenic and inorganic origin deposited both in marine and non-marine environments. The reliability of ages from the latter is restricted by uncertainty regarding the value of the initial ratio. In non¬marine areas, this factor shows time-dependent variations since shells of some nonmarine mollusks actually acquire uranium after the death of the organisms. However, since groundwater can enrich in 234U relative to its parent, this enables its specific sources to be assessed. In addition, mixing of different water masses character¬ized by their individual (234U/238U) activity ratios can be determined (Kronfeld and Rosenthal 1981).