Isotopic dilution analysis is a powerful method of determining small amounts of material in a form where 100% separation and recovery of the material is difficult. In principle a quantity of radioactive material of the same chemical form and of known specific activity is added to the unknown amount of inactive material. Determination of the specific activity of the mixture then allows calculation of the quantity of inactive material present. Suppose we have x grams of a radioactive material of activity A1 dpm and a molecular weight M1. The specific activity (S) of this material is:

If y grams of chemically identical, but inactive, material is added the final specific activity becomes:
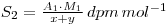
If a chemical reaction is now performed, resulting in a change in the chemical form of the material (e.g. S*O42- → S*2-, where the * indicates the radiolabelled element), 9 then the specific activity of the new chemical form will still be S2, even though some of the material may have been lost in performing the reaction. Thus, if the weight of material recovered is z grams, then:
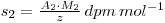
Where A2 is the activity of the recovered material and M2 is the molecular weight of the new chemical form. If y had been the unknown quantity, its value may now be determined, since:
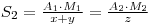
Therfore:
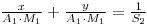
Therfore:
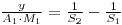
And Since:
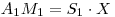
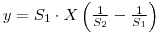
therfore:
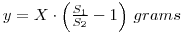
In this experiment, a variation on the above is required since the weight of the radioactive material is unknown. You are provided with a solution containing y g dm-3 of phosphate mixed with an unspecified amount of chloride impurity. A measured volume of the solution is mixed with radiolabelled 32P-phosphate and a volume of the mixture, V1 is evaporated and counted. If the activity of the material is A1 dpm, then the specific activity of the phosphate (molecular weight M1) is:
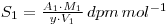
The mixed solution is then reacted with ammonium molybdate so that a precipitate of ammonium (12) molybdosphosphate ((NH4)3PO4.12MoO3) is formed. A known mass of this precipitate (W2 grams) is counted, and the resulting activity, A2, used to determine the specific activity of the molybdosphosphate (molecular weight M2).
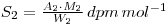
As before the specific activities are the same, so that:
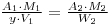
and
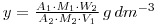
Thus, we have determined the phosphate concentration of the solution provided for assay. Note that the mass of phosphate in the original carrier free 32P-phosphate solution has been neglected in this calculation. In fact, the mass per cm3 of 32P-phosphate in this solution would be in the 10-9 – 10-12 g range, and can justifiably be neglected in comparison with y. For the calculation you will need to calculate the molecular weights of the phosphate (as Na2HPO4) and the molybdophosphate (as (NH4)3PO4.12MoO3).