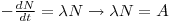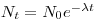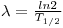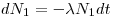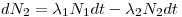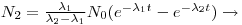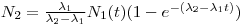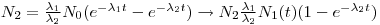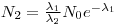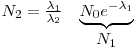Radioactive disintegration is a stochastic process, which means a random process that can be described statistically. Here you will learn about the secular radioactive equilibrium, and how any measure of a radioactive source is stated with uncertainty.

The Basics - A Single Radioactive Nucleus

In a sample with N radioactive atoms of a particular nuclide, the number of nuclei that disintegrates with the time dt will be proportional with N, see eq. 1:
-\frac{dN}{dt} = \lambda N \rightarrow \lambda N = A
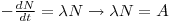
 eq. 1
where λ is the disintegration constant and A is the rate of disintegration.

Eq. 1 is a simple differential equation and can be solved using standard mathematical techniques. The solution is written:
N_{t}=N_{0}e^{-\lambda t}\,
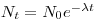
 eq. 2
N0 is the number of nuclei at present at t = 0. The time when half of the nuclei has disintegrated is called the half-life.

At t = T1/2 then N = N0/2. If we insert this into eq. 2 the following connection between the disintegration constant and the half-life is obtained:
\lambda = \frac{ln2}{T_{1/2}}
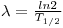
 eq. 3
The half-life is a characteristic value for each radioactive nuclei.

Decay Chains and Mother-Daughter Relationships

A radioactive nuclide will often disintegrate into a product that is radioactive as well: Nucleus 1→Nucleus 2 →Nucleus 3. The initial nucleus is usually referred to as the mother nuclide and the product as the daughter nuclide.
Assume that at the time t = 0, N0 of the mother is N1(t =0), N2(t=0) and N3(t=0), the change in number of mother- and daughter nuclei can then respectively be described through Eqn 4 and Eqn 5:
dN_{1}=-\lambda N_{1}dt\,
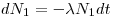
 eq. 4

dN_{2}=\lambda_{1}N_{1}dt-\lambda_{2}N_{2}dt\,
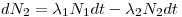
 eq. 5
The solution of Eqn 4 is already known, it is the expression in eq. 2 while the solution for the amount of daughter nuclei are given with:
N_{2} = \frac{\lambda_{1}}{\lambda_{2} -\lambda_{1}} N_{0} (e^{-\lambda_{1} t} -e^{-\lambda_{2}t}) \rightarrow
N_{2}= \frac{\lambda_{1}}{\lambda_{2} -\lambda_{1}} N_{1}(t) ( 1 - e^{-(\lambda_{2} - \lambda_{1}t)})
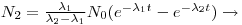
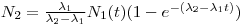
 Eqn 6

If the half-life of the mother is much less than that of the daughter, Eqn 6 can be simplified into:
N_{2} = \frac{\lambda_{1}}{\lambda_{2}} N_{0} (e^{-\lambda_{1} t} -e^{-\lambda_{2}t}) \rightarrow N_{2} \frac{\lambda_{1}}{\lambda_{2}}N_{1}(t) (1-e^{-\lambda_{2}t})
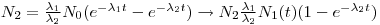
 Eqn 7

where 1-eλ(2)t is the saturation factor and λ2-λ1~λ2. The above equation can be further reduced by the assumption that t >> T ½(2) (the observed time is much larger than the daughters half-life).
N_{2} = \frac{\lambda_{1}}{\lambda_{2}}N_{0}e^{-\lambda_{1}}
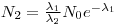
 Eqn 8

\begin{matrix}& N_{2} = \frac{\lambda_{1}}{\lambda_{2}} & \underbrace{N_{0}e^{-\lambda_{1}}} \\ & & N_{1} \end{matrix}
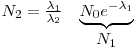
 Eqn 9

When eλ(2)t→0, eqn 9 is called a secular radioactive equilibrium and can be written as λ2N2 = λ1N1.