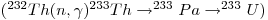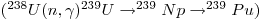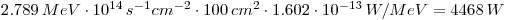Exercises with Particles and Nuclear Reactions
1:
- Thermal neutrons have a kinetic energy of about 0.025 eV
- Fast neutrons are slowed by elastic collisions with particles with the similar mass as the neutrons. A moderator also needs to have a low cross-section for absorbing neutrons.
- A moderator is a material that slows down the neutrons, for instance H2O, D2O, C, Be. A neutron absorbent catches the neutrons and reacts with the neutron. Good absorbents are e.g. borium and gadolinium.
- The reaction 3He+n→3H++1H(+2e-). The charged particles from the reaction creates more ionizations when they travel towards the anode and the cathode, this gives a electric signal.
- The Q-value from the reaction is 763 keV, the reaction is exothermic.
- 3H+ and 1H+ is created.
- From the nuclide carte we can see that 3He has a high cross-section for the n,p-reaction.
- The two products in the reaction receive opposing recoils 180 degrees. Conversion of momentum m1v1=m2v2 gives:
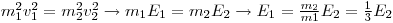
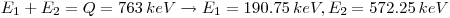
2:
- Q-Value 2.224 MeV
- And 3. The energy of the deuterium is not calculated relativistic but the γ-ray is completely relativistic, we then get:
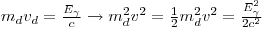
Inserting the energy of the deuterium we get:
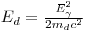
We know that
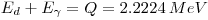
solving for this:
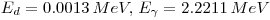
3:
Q-Values
- 40Ca: M(40Ca)+M(α)-M(44Ti)=5.13 MeV
- 52Cr: 7.61 MeV
- 56Fe: 6.29 MeV
- 58Ni: 3.37 MeV
4:
For ground state transitions assuming zero momentum to the neutrino
- 0.16 MeV
- 0.78 MeV
- 1.655 MeV subtracting the mass of a electron and a positron we end up at 0.633 MeV.
- β- :0.579 for 64Zn, β+ : 0.653 MeV for 64Ni.
- The cause of this effect is the even-even/odd-odd addition to the energy
- 228Ra is created with disintegration of 232Th: 232Th→228ra + α +Q this gives
M(228Ra) = M(232Th)-M(α)-Q
All of the natural thorium that exist is 232Th. The mass that is given for thorium is therefore more or less equal to the mass 232Th 232.0381 u. It is much the same for helium where the mass is 4.002602 u. To find M(228Ra) we need to find the Q-value. The Q-value is distributed as kinetic energy on the products 228Ra and alpha. The alpha particle has very little mass compared to 228Ra, and the alpha particle by conversion of momentum will receive almost all the kinetic energy:
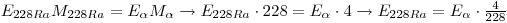
Eα is known (using the most powerful α for transition to ground state), and the Q value is found
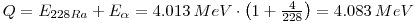
This gives:
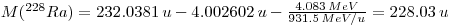
5:
- 6:**
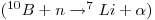
- Q-value is 2.789 MeV
7:
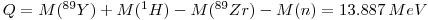
- 1 GBq 89Zr = 4.1•1014 atoms, there must be created 1.9•1010 per second
- Yttrium is a mono isotope, you will only find 99Y in nature. Therefore there is no need to purify the sample for other isotopes.
| Page | Date Edited |
|---|---|
| Calculation Exercises | Oct 14, 2015 |
| Suggested Solutions to Particles and Nuclear Reactions | Nov 5, 2014 |