

1:
- 1000g Th(NO3)4
2.083 mole ⟶ N(Th)
1.25•1024atoms. This is natural thorium, where the equilibrium in Th-series will lead to equal activity of 232Th and 228Th. Since 232Th has a incredibly long half-life and 228Th is short compared to this and we can approximate N(Th)≈N232Th)=1.25•1024The disintegration for both is 1.96•106Bq. - 6.46•10-8g
- 10000 Bq228Ra = 2.62•1012atoms = 90%⟶100% 2.91•1012atoms. If232>Th is N1and 228Ra is N2we can use the formulas for mother/daughter relations:
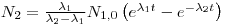
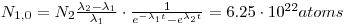
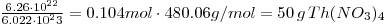
lternatively it can be solved by using D(228Ra) = 11 111Bq:
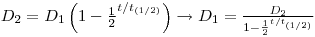

- 228Ra is formed from 228Th, an immeasurable amount of 228Th is formed in three days, and formation of new 224 Ra can therefore be ignored. D0(224Ra)=D0(228Th)=1.36•106Bq. and we get a normal decay:
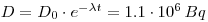
- 228Ac,220Rn,216Po, 212Pb, 212Bi, 212Po.
2:
- When T= 0 only the natural isotopes of uranium is present: 238U,235U and 234U.
- D/(span style="font-size: 75%; vertical-align: super;">238U)=D(234U) ≈ 12.5 kBq, D(235U) = 575 Bq.
- When t = 23.5 h there is created some 234Th and some 234Pa, but creation of other daughters from 238U is negligible. From the 235U there is created 231Th
- D(238U) = D(234U) =D0,> D(234Th) = D(234Pa) = 376 Bq,
D(235 U) = D0,
D(231Th) = 287.5 Bq. - When t = 23 days the same radionuclides are present.
- D( 238U) = D( 234U) =D0,
D(234Th) = D(234Pa) = 6250 Bq,
D(235U) = D0,
D(231Th) = D(235U) =575 Bq. - When t = 1.0 y the same radionuclides are present.
- D(238U) = D(234U) =D0,
D(234Th) = D(234Pa) = D(238U) = 12,5 kBq,
D(235U) = D0,
D(231Th) = D(235U) =575 Bq. - When t = 10.0 y the same radionuclides are present.
- same as 8.
3:
1: The shale contains all of the daughter products from 238U and 235U in equilibrium. In 10 g natural Uranium there is 125 kBq 238U and 5.75 kBq 235U which gives:
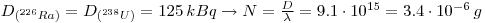
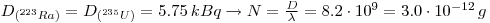
2: 210Pb exist as a daughter from 238U:
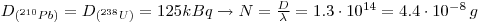
3:One of the daughters is210Po, which is a alpha emitter and can do great harm inside the body. In addition Pb is a daughter of radon which makes it possible for it to enter the lungs.
4:
- It is easily accessible; it only needs to be processed once to create several doses of medicine.
- 100 Mbq 201Tl = 3.79•1013atoms → m = 1.27•10-8g.
- The amount inserted is too small to be considered poisonous for humans.
5:
- After one half-life it will be 50 Mbq, which is 3.92 h (44Sc).
- D1(44Ti) ≈ D0(44Ti) = 100 MBq, m(44Ti) = 2.01•10-5g
6:
- The gamma radiation comes from the daughters 228Ac and 208Tl.
- There are 2 radioisotopes in natural Thorium, namely 232/228Th. They are in a secular equilibrium and the activity of the latter will be equal to the activity of the former. It is about 7.34•109more mass of232Th than 228Th.
- To achieve equilibrium through the whole series it needs to have taken ten times longer than the most long-lived daughter; for238U this is 2.455•106y for 235U it is 3.276•105y and for 232Th 57.5 y
7:
- 100 g natural Th is more or less only 232Th, this gives a decay of 405.9 kBq. D(229Th) = D(232Th), D(total) = 811.8 kBq.
- 405.9 kBq is 1.34•10-8g.
- Nothing – 229Th does not exist in nature.
- After 7.2 days the activity of 228Ra will be 963 Bq and it will be in equilibrium with 228Ac.224Ra is formed from 228Th and after two half-lives there will be 75% of max possible 224Ra in equilibrium with 210Rn, 216Po, 212Pb, 212Bi (assume 50% branching to 208Tl and 212Po). Total alpha activity: 2.2029 MBq, beta-activity: 610.7 kBq.
8:
- 5.78 hours.
- After two half-lives, 76 hours, there will be 75%, 7500 Bq.
9:
- The alpha decay of 211At gives 207Bi, with a half-life of 31.55 years.
- 6.57•10-7g
- After one week all of the 211At will decay to207Bi. The half-life is long enough ( 31.55 years) to do the approximation N(207Bi) ≈ N0(211At)=1.87•1015
7:
- 100 g natural Th is more or less only 232Th, this gives a decay of 405.9 kBq. D(229Th) = D(232Th), D(total) = 811.8 kBq.
- 405.9 kBq is 1.34•10-8 g.
- Nothing – 229Th does not exist in nature.
- After 7.2 days the activity of 228Ra will be 963 Bq and it will be in equilibrium with 228Ac. 224Ra is formed from 228Th and after two half-lives there will be 75% of max possible 224Ra in equilibrium with 210Rn, 216Po, 212Pb, 212Bi (assume 50% branching to 208Tl and 212Po). Total alpha activity: 2.2029 MBq, beta-activity: 610.7 kBq.
Back to exercsies