The purpose of this exercise is to study how the nuclear waste that is not fission fragments is generated in a nuclear reactor. For this purpose a computer program will be written that simulates the nuclear reactions and disintegrations inside a nuclear-reactor core loaded with a specific fuel mixture. To keep the exercise doable within the alloted time we will introduce a number of simplifications. Nevertheless the simulation will provide important understanding and insight into the dynamics of a running nuclear reactor. The main simplification used is that only thermal neutrons are present in our simulated reactor.

Learning Outcome

Performing this exercise should provide you with:

Limitations

Many aspects of constructing and operating a nuclear reactor is not considered in this exercise. In particular, the importance of considering the effect neutron energy has on fission and n-capture cross-section is ignored. Furthermore, the effect of in-growth of neutron-absorbing nuclei ("poisons") is ignored. This exercise is not intended for - and will not convincingly model - the neutron inventory of a nuclear reactor. This said, the simulation is quite useful in explaining and illustrating all the problems associated with nuclear waste.

Introduction

In a nuclear reactor one should think that only fission framents should be left after having "burned" the nuclear fuel. However, this is not true since neutron capture in the fuel also will produce heavier actinides. In fact, transurans produced when burning uranium fuel is one of the major obstacles in handling spent nuclear fuel. An additional concern to the radiotoxity of the waste is also the accumulation of plutonium that can be used for nuclear weapons.

To do laboratory tests with fuel mixtures to investigate the compositin of the nuclear waste is extremely difficult and expensive, for obvious reasons. Therefore, we can not do such investigations as hands-on exercises in a course, but what we can do is to use a computer to simulate the processes that takes place inside the reactor core. To do so at an accuracy level that exactly models the reactor is highly complex and computer intensive, but if we accept a slightly less accuracy level the simulations can made simple enough to be run on a ordinary computer within a reasonalbe time. Thsi is what we will do in this exercise.

Theory

You might want to read up on the following theory before you start this exercise:
You should be able to find textbook material on these topics in your course book(s), on the internet and also on NucWik. In the following we assume you have a good basic knowledge of these topics.

As the fission process proceeds inside the reactor core, both fission fragments (the two halfs left over after splitting the fissionable nuclei) and high-energy neutrons are released. The neutrons are, in a ordinary reactor, "cooled down" (i.e. their energy is reduced) until they only have "termal" velocities (i.e. move with the same speed as any other atom at that particular temperature). The reason the neutron must be cooled down is because they are more reactive (have a higher cross-section) as thermal neutrons than as high-energy neutrons. Of course, in a real reactor also the high-energy neutrons will to some extent be reactive, but in this exercise we will ignore that - we only consider thermal neutrons.

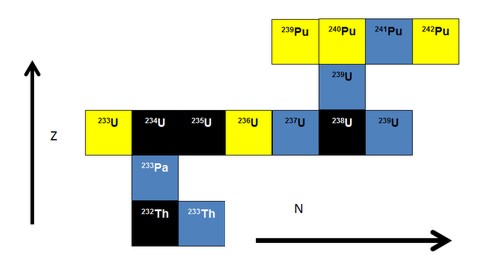Simplifed nuclear chart for uranium area.jpgThe thermal neutrons will induce fission in the fuel nuclei and thus sustain a chain-reactions that keeps the reactor running. However, thermal neutrons will also be captured by nuclei present in the fuel. This can be the fissible nuclei (like 235U) or nuclei just being present in the fuel (like 238U). This process will lead to a buildup of a large number of heavy nuclei (not fission fragments) that were not present in the fuel at the start. For example if 238U captures a neutron 239U is produced. Now, these new nuclei are radioactive and will disintegrate according to their respective half-lives. This leads to creation of even more new nuclei. For instance, the 239U just mentioned will disintegrate by beta-minus decay and create 239Np. In principle, the 239U - if it survives long enough before disintegrating - could also capture a second neutron and that would produce 240U. If the reactor is operated long enough, which is normally the case, the buildup of all these transuranium nuclei can be quite extensive. Since some of them have very long half-lives they add significantly to the time the nuclear waste is going to be radiotoxic. A simplified picture of the most important nuclei being produced in a nuclear reactor burning uranium or thorium is shown to the right. The black nuclei might be present in the fuel at the start (we will investigate different mixtures), the yellow ones decay by alpha emission and the blue ones with beta-minus emmision. You should check out your nuclear chart to see more details and try to understand the dynamics.


Simulation Algorithm

Instead of all the coupled equations linking everything together, we will take the following approach:
  1. We set up a matrix representing the relevant part of the nuclear chart (e.g. from thorium and up). Each element in the matrix represent one nuclei (like the nuclear chart).
  2. We will assume a constant neutron flux during the entire operation (gross simplification), and only thermal neutrons at that. We assume the reactor remains critical until we switch it of.
  3. Each matrix element (representing a given nuclei) should specifiy the amount of that nuclei being present in our "reactor". In addition, you would probably want to store relevant parameters for each nuclei in the same matrix element (using a suitable feature of your programing language to do so (e.g. in LabView we will use a "cluster"). The relevant paramters are:
    1. The cross-section for neutron capture
    2. The cross-section for neutron induced fission
    3. The half-life of the nuclei
    4. The type of decay, including branching information if there are more than one type of decay.
    5. In addition, you might find it useful to also write down the atomic mass number (can also be calculated from position in matrix)
    6. Depending on how you have defined your matrix, the N and Z for the nucleus can be useful
  4. Initially, only the nuclei in the fuel will be present, all the other nuclei (matrix elements) will be empty (zero).
  5. We will now use the computer to "update" the matrix as the reactor is running. We will do this with a fixed time interval between each update. Each time the computer "updates" it should do the following for each single matrix element:
    1. Use the given neutron flux and calculate how much has fissioned in the last time interval (if fission is possible). Subtract this amount.
    2. Use the given neutron flux and calculate how much of the neighbouring nucleus has been produced due to n-capture. Update both the current matrix element and the neighbouring one accordingly.
    3. Calculate how much of the nuclei has decayed during the last time interval. Subtract this amount and add it to correct matrix element according to the type of decay.
  6. Repeatedly update the matrix until you have reached the desired operation time.

Provided the time intervals are kept short (experiment!) we should not get any big error due to changes taking place within a time interval. E.g. if the time interval is longer than the half life for a given nucleus, then that nucleus will be gone before the calculations are performed. However, in reality some of the nuclei could have undergone n-capture or fision before they decay. But if we keep the time interval short enough such effets should not be a problem.

You should also do the matrix update on a copy of the main matrix, because due to n-capture and decay some elements will change before the algorithm have updated them. When all elements have been updated you copy the data back into the main matrix.

You can solve this problem in most computer languages. Use the one that are available to you and that you have learned. We will not teach you programming skills in this exercise - we want you to use skills accuired in previous courses. Remember to test each part of your code thoroughly and advance in small steps, making sure that each step is working correctly before you proceeed.

Problems to Investigate

Once your code work correctly, you can start to investigate how a nuclear reactor behaves under different conditions. Investigate the following scenarios:
  1. Effects of fuel composition. For a thermal n-flux of 10^15 n/s and one year reacotr operation, investigate the following fuels
    1. 3% enriched 235U
    2. Pure 235U
    3. 20% 233U and 80% 232Th
    4. Pure 239Pu
  2. Investigate the composition of the waste for the different fuels after 1, 10, 100, 1,000 and 100,000 years storrage. You do this by "running" the reactor with zero n-flux. For the long times you might want to increase the time-step size (why?).
  3. For the 3% enriched 235U fuel, investigate the effect of differenct n-fluxes: Calculate waste after one year operation for 10^14, 10^16 and 10^18 n/s.

The results should be represented graphically and you should write a report which discuss the results and compare them to each other. What have you learned about operation of reactors and the resulting waste composition?

Some Further Programming Tips and Suggestions


Your program should be able to do:

  1. The n-flux used in the program must be changeable
  2. The program will be much more easy to use (and debug!) if it can fetch initial data and parameters from a file. The file should be written in ascii (plain text) so you can edit it with a normal text editor (take care that you store it as plain text if you use an advanced text editor like MS Word).
  3. Similarily, it will be convenient if the program outputs the final results in a text file which can be inspected, printed and imported into suitable plotting software.

Added features could be:
  1. Stop the calculations before the total time has elapsed (in case it takes for ever to do the caluclations
  2. Have the ability to display the result in different units: Bq or GBg, kg or g and number of atoms
  3. Graphical display of trends

Additional Exercises


  1. Compare the waste from the previous reactor to a reactor using: 20% Thorium 4% 235-U and 76% 238-U as fuel.Show the activity of Th, Pu, Am and Cm after: 1 year, 10 years, 100 years and 1000 years.
  2. You have one tonne MOX fuel with 7% plutonium and 93% Uranium. How much will the waste composition change with the flux of: 1010,1012 and 1014? The composition of the plutonium and uranium is given in the tables below.


The plutonium used consist of
Nuclei name
 Amount wt%
238-Pu
 1
239-Pu
 60
240-Pu
 25
241-Pu
 9
242-Pu
 5

And the uranium consist of
Nuclei name
 Amount wt%
234-U
 0,003
235-U
 0,25
236-U
 0,001
238-U
 99,74