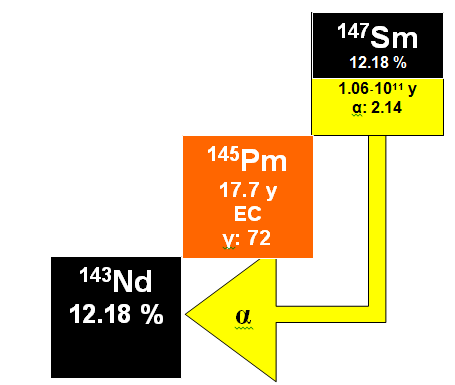
Both of these elements are lanthanides (rare earth elements) and each has twenty-six isotopes of which seven occur naturally. Samarium-147 is radioactive and decays by a emission to a stable isotope of neodymium, 143Nd:



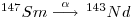
The half-life of 143Nd is 1.06•1011 y with a corresponding decay constant of 6.54• 10-12 y-1 and the decay scheme is applicable to dating terrestrial rocks, stony meteorites and lunar materials.

Samarium, neodymium and the other rare earth elements occur in high concentrations in minerals such as monazite (CePO4) and as trace elements in common rock-forming ones such as biotite and plagioclase feldspar. The atomic [Sm/Nd] ratio on Earth varies from 0.1 to 0.5 and the relative abundances are 15 % for 147Sm and 12.18 % for 143Nd. It has been suggested that neodymium is more concentrated than samarium during the fractional crystallization of magma and that crustal rocks usually have lower [Sm/Nd] ratios than rocks originating from the upper mantle such as oceanic tholeiites. Also, during the formation of silicate liquids by partial melting of rocks in the crust or mantle of the Earth, the liquid phase may enrich in neodymium relative to samarium. This may be because Nd3+ has a larger ionic radius than samarium which gives it a lower ionic potential as a result of which it forms weaker ionic bonds that can be more easily ruptured than those involving Sm3+.

The growth of radiogenic 147Nd due to the decay of 147Sm can be given as:

eqn 1

where 144Nd acts as the reference since the number of its atoms in a unit quantity of any given sample remains constant so long as the host system remains closed to neodymium. The decay constant of 147Sm, λ, is taken to be 6.54•10-12 y-1.

Determination of ages by the Sm/Nd method entails analyzing either individual minerals or cogenetic rock suites in which the ratios between the two are sufficiently different to define the slope of an isochron in coordinates of [Nd/144Nd] and [Sm/144Nd]. The method is especially suitable for mafic and ultra-mafic rocks, cf. the Rb/Sr method which is best suited for acidic and intermediate igneous rocks enriched in rubidium and depleted in strontium. Since the rare earth elements are less mobile than the alkali metals and the alkaline earths, phenomena such as regional metamorphism have less effect on them. Hence suitable rocks can be dated by the Sm/Nd method even if they have lost or gained rubidium and strontium and this makes the Sm/Nd method a useful complement to the Rb/Sr method.

Apollo-12, ADOR and CHUR

Volcanics from the Onverwacht Group, Swaziland and South Africa, comprise the basal part of the Early Precambrian Barberton greenstone belt found both in Swaziland the Transvaal. Data from them gave an age of about 3.54 Ga calculated using an initial [143Nd/144Nd]o ratio of 0.50809 ± 00004 (Hamilton et al. 1979). The strontium and neodymium isotopic record of Apollo-12 basalts from the Moon were examined. Isochrons were derived for an achondrite (eucrite) and another meteorite and gave ages of about 4.58 Ga and 4.562 Ga, respectively, with primordial [143Nd/144Nd]p ratios of 0.50684 ± 0.00008 and 0.506664. An initial [87Sr/86Sr]o ratio was termed ADOR. The isotopic evolution of neodymium in the Earth has been described by means of a model termed CHUR (CHondritic Uniform Reservoir). And the present value of the [143Nd/144Nd] ratio is 0.512638 relative to a [146Nd/144Nd] ratio of 0.7219. The present value of the [147Sm/144Nd] ratio of CHUR is 0.1967 which permits calculation of [143Nd/144Nd] ratio in any past time interval.