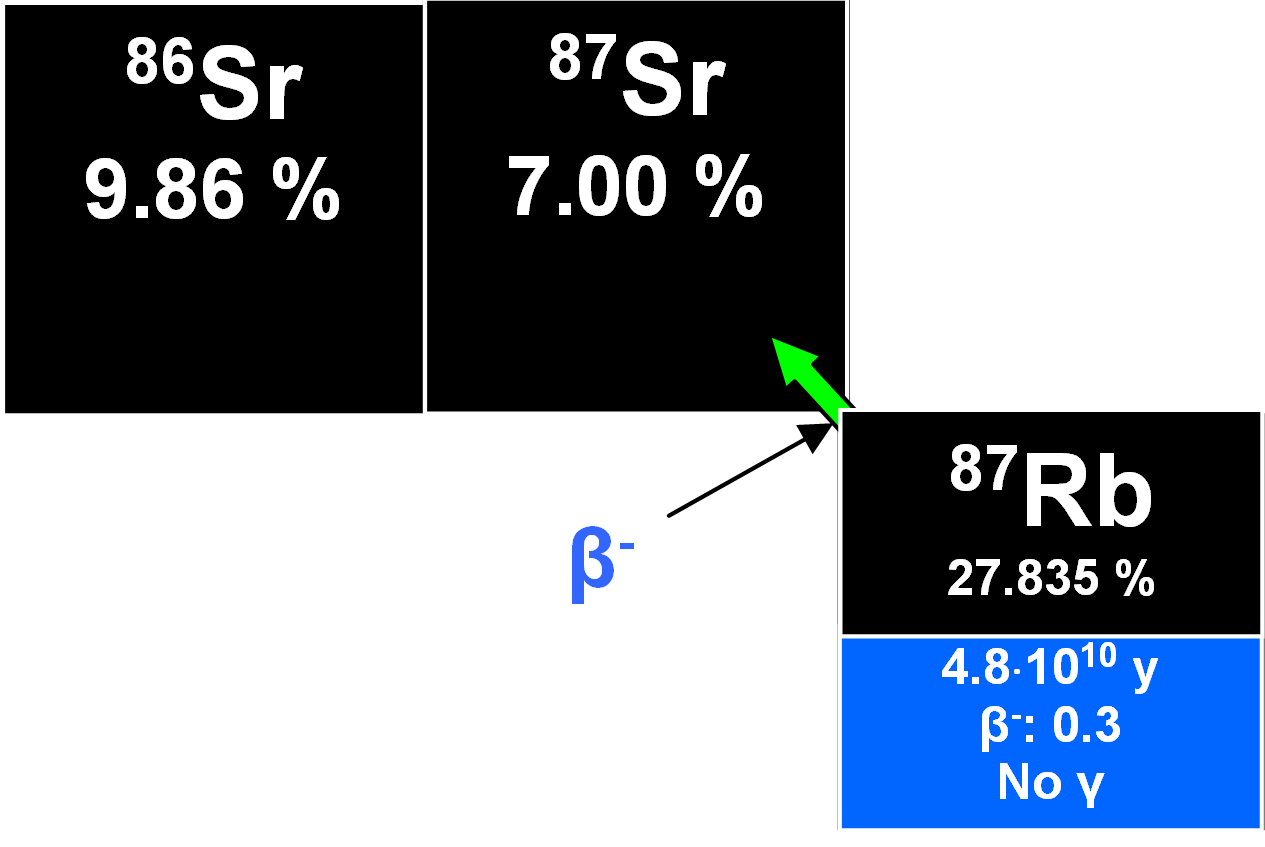
Rubidium has an ionic radius sufficiently close to that of potassium so that it can substitute for the latter in all potassium-bearing minerals. Hence, it occurs as a dispersed element forming measurable parts of micas, potassium feldspar, some clay minerals and evaporites. Two isotopes occur in nature, namely 85Rb and the the long-lived radioactive 87Rb with isotopic abundances of 72.17 % and 27.83 %, respectively. 87Rb decays by β-- emission to 87Sr with a half-life of 4.8•10 10 y.
The decay process is:

where Qβ = 275 keV.
Strontium has four naturally occurring isotopes, 87Sr having a relative abundance of about 7 % and a metastable state with a γ-energy of 388 keV for the isomeric transition with half-life of 2.81 h. The abundance of 87Sr varies however, reflecting the formation of radiogenic 87Sr by the decay of 87Rb. Therefore, the precise isotopic composition of strontium in a mineral or rock containing rubidium depends on the age and the [Rb/Sr] ratio.
The growth of radiogenic 87Sr in a rubidium-enriched mineral over a time interval t is given by the following expression:
![[^{87}Sr]_t=[^{87}Sr]_0+[^{87}Rb]_t\cdot(e^{\lambda t}-1) [^{87}Sr]_t=[^{87}Sr]_0+[^{87}Rb]_t\cdot(e^{\lambda t}-1)](math/a249f34152d1b9ec138f672a4d98efdd.gif)
where [87Sr]t and [87Rb]t are the total numbers of atoms of the respective isotopes in a unit mass of the mineral now (t) and [87Sr]0 is the amount of 87Sr incorporated into the mineral when crystallized, λ is the decay constant of 87Rb and t is the age of the mineral sample.
An equation for age determination has been presented and based on real isochrons. A rubidium/strontium three-isotope plot (see following figure ) is constructed involving [87Sr/86Sr] against [87Rb/86Sr]. When a rock cools, all of its minerals have the same ratio of 87Sr to strontium-86 though they will have varying amounts of rubidium. As the rock ages, rubidium decreases by changing to 87Sr. For any given age, the composition can be represented by a line through the points and this line can be extrapolated back to zero to obtain the initial [87Sr/86Sr]o ratio. This ratio is about 0.70775, but for the K/T Boundary it is 0.70790, a rise attributed to acid rain. Values at this boundary have been given as 1.6 for Denmark, 1.3 for Colorado and 1.1 for New Zealand. The age of the rock is determinable from the slope of the isochron. This slope is a monotonic function of the age of the rock and the older the rock, the steeper the line. If the slope of the line is m, the age t is given by:
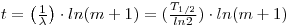
Measuring rubidium and strontium concentrations in suitable minerals can be effected using standard chemical and mass spectrometric procedures, X-ray fluorescence or isotope dilution.
Real isochrons may be altered through metamorphism when heat causes minerals to deviate from the whole-rock isochron and each acquires its own isochron. Also, new minerals may form and existing minerals may re-crystallize. The entire situation is one of mobility entailing ionic diffusion. Metasomatism may occur and involve both the bulk chemical composition and the trace element composition. The phenomenon can affect the parent/daughter relationships of all naturally occurring radioactive element systems in a particular rock. A suitable age equation for t is available and, to implement it, the best rocks to utilize are igneous acidic ones such as granite because they contain both micas and potassium feldspars. However, both concordant and discordant results may be obtained. The latter are due to gain or loss of radiogenic 87Sr caused by geological events usually connected to metamorphism. And when forming, such igneous rocks undergo fractional crystallization of magna involving the separation of crystals from an ever-diminishing liquid magma so that suites of co-magmatic igneous rocks have different chemical compositions. However, if it is assumed that the strontium in such a magma stayed isotopically homogeneous through the cooling process, all the various suites formed will have the same initial [87Sr/86Sr]o ratio. It is reasonable to assume that all rocks formed will have about the same age because cooling and crystallization times are negligible compared to the age of the event. In this way, the age equation may be regarded as relating to a set of suites and creating a group of straight lines on a plot having a slope intercept such that:
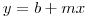
All rock samples from a co-magmatic suite plot as points on a straight line in coordinates of [87Sr/86Sr] (y) and [87Rb/86Sr] (x), that is to say that they form an isochron. Its slope is related to t thus:
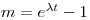
and the value of the initial [87Sr/86Sr]0 ratio may be provided by the y-intercept b.
Fictitious isochrones in the Rift Valley
Fictitious isochrons have slopes devoid of any geochronological significance. If a set of samples resulted from the mixing of two components with different [87Rb/86Sr] and [87Sr/86Sr] ratios, they will fall on a straight line which links the end members in coordinates of these ratios. The result is a fictitious isochron which may have a positive or a negative slope depending on the relative values of the end members. An instance was obtained from potassic lava flows found in volcanic centers lying along the western Great Rift Valley north of Lake Tanzania and west of Lake Victoria, these centers being about 160 km apart (Bell and Powell 1969). Identified as Pliocene to Recent in age, their volcanic activity is believed to have continued into historical times so there is no doubt that the relevant rocks are young and ought to give an isochron with practically zero slope. However, a significant positive correlation between the average [87Sr/86Sr] and the [87Rb/86Sr] ratios of the rock types was found and the straight line drawn through the data points was not an isochron, rather a mixing line. It had a slope yielding a fictitious age of 773 Ma because the [87Sr/86Sr] ratios of the rocks resulted from mixing and do not relate to the radioactive decay of 86Rb in them after crystallization took place.
Meteorites, BABI, LUNI and Fun
Rubidium/strontium analyses of chondritic meteorites gave an average age of about 4.49 Ga as did those of achondrites and it was suggested that crystallization occurred fast and that they had similar initial [87Sr/86Sr]o ratios. Basaltic achondrite analyses gave the value for the primordial [87Sr/86Sr]p ratio of 0.6987 ± 0.00003 and this is termed BABI (Basic Achondrite Best Initial). Isotope anomalies in meteorites imply that the solar nebula could not have been isotopically homogeneous with respect to some elements. The concert of Fractionation and Unknown effects as possible causes produced the term FUN (Papanastassiou and Wasserburg 1969). The Rb/Sr method was used to help in unveiling the seismological history of the Moon and an age for the satellite of about 4.5 Ga was obtained. BABI is paralleled by LUNI of which a value has been given as 0.69892 ± 0.00009 (Nyquist 1977).
Some Caveats
It must be added that there is a number of things that can present difficulties for the Rb/Sr dating method and include the following. One is the case where a rock contains some minerals that are older than the main part of the rock. Occasionally magma inside the Earth will take up un-melted minerals from the surrounding rock as it moves through a magma chamber. Normally such 'xenoliths' are distinguishable from the younger minerals surrounding them. If they are not used for dating the rock, the points represented by these minerals will be off the line made by the rest of the points. Another problem arises if a rock has suffered metamorphism during which it became extremely hot but not sufficiently hot to completely re-melt the rock. Then, dates will be confused and not lie along a line. Some minerals will have completely melted others not at all. Thereafter some minerals will try to give the igneous age while some others will try to give the metamorphic age. In such cases, there will not be a straight line and no valid date is determined.
In some rare cases, the Rb/Sr method gave straight lines giving wrong ages. This may result when the rock being dated was formed from a magma that was not well mixed and had two separate batches of rubidium and strontium. One magma batch had rubidium and strontium compositions near the upper end of a line and one batch had compositions near the lower end of the line. Then, the minerals received a mixture of both batches and the resulting composition ended near a line between the two batches. Such a state of affairs is termed a two-component mixing line. Among tens of thousands of rubidium/strontium dates, at least thirty cases have been documented. Of course, if a two-component mixture is suspected, a second dating method must be employed in order to either confirm or disprove the rubidium/strontium date. In general, it may be stated that agreement between several dating methods is by far the best way to date rocks.