Basic Theory
A radionuclide generator, also popularly called a “cow”, is composed of a mother-daughter radionuclide relationship where the mother has a longer half-life than the daughter. The daughter is continuously produced by decay of the mother in the generator system, and the daughter can be separated (“milked”) from the generator by chemical or physical methods. In this Exercise we are going to use one such system defined in more detail below.From basic lectures on decay we have the following relation between a radioactive nuclide and its radioactive daughter:
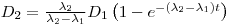 |
1 |
Where D2 is the amount of the daughter species, λ2is the decay constant of the daughter, λ1is the decay constant of the mother, t is the time.
If λ1 << λ2, i.e. the half-life of the daughter is much shorter than the half-life of the mother, we have:
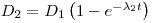 |
2 |
If the growing-in time t on the generator in (2) is much longer than the half-life of the daughter (T½,2), the exponent will go towards the limit of 0. This again results in the fact that the disintegration rate of the daughter equals the disintegration rate of the mother on the generator, i.e. the maximum activity that can be produced of the daughter on the generator equals the activity of the mother. Expressed in mathematical terms for (2):
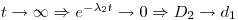
At this situation we say that we have obtained radioactive equilibrium in the generator system. A practical equilibrium is defined to be reached when t ≤ T½where D2≤ 0.999•D1.
Practical Approach
In general, it is not practical to wait until radioactive equilibrium has been reached before utilizing the generated daughter activity in laboratory experiments. By using thatλ2=ln 2 / T½,2 and setting
t= T½,2 into (2), we obtain:
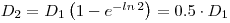
i.e. we have obtained 50% of the maximum obtainable activity already after a growing-in time of one daughter half-life.
Fig.1 illustrates how the activity of the daughter increases as a function of the growing-in time in units of T½,2:
In the lab exercise where we made a calibration source from uranium, we used the granddaughter of 238U (as U3O8) to get a high-energy beta emitter. The first part of the 238U natural radioactive series may be written as
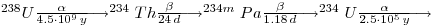
We observe that this part of the series gives possibility for two generator systems, i.e.238U ⇒ 234Th and 234Th ⇒ 234mPa. The first is not practical in short laboratory exercises because of the relatively long half-life of the daughter (24 d), but the second system is suitable.