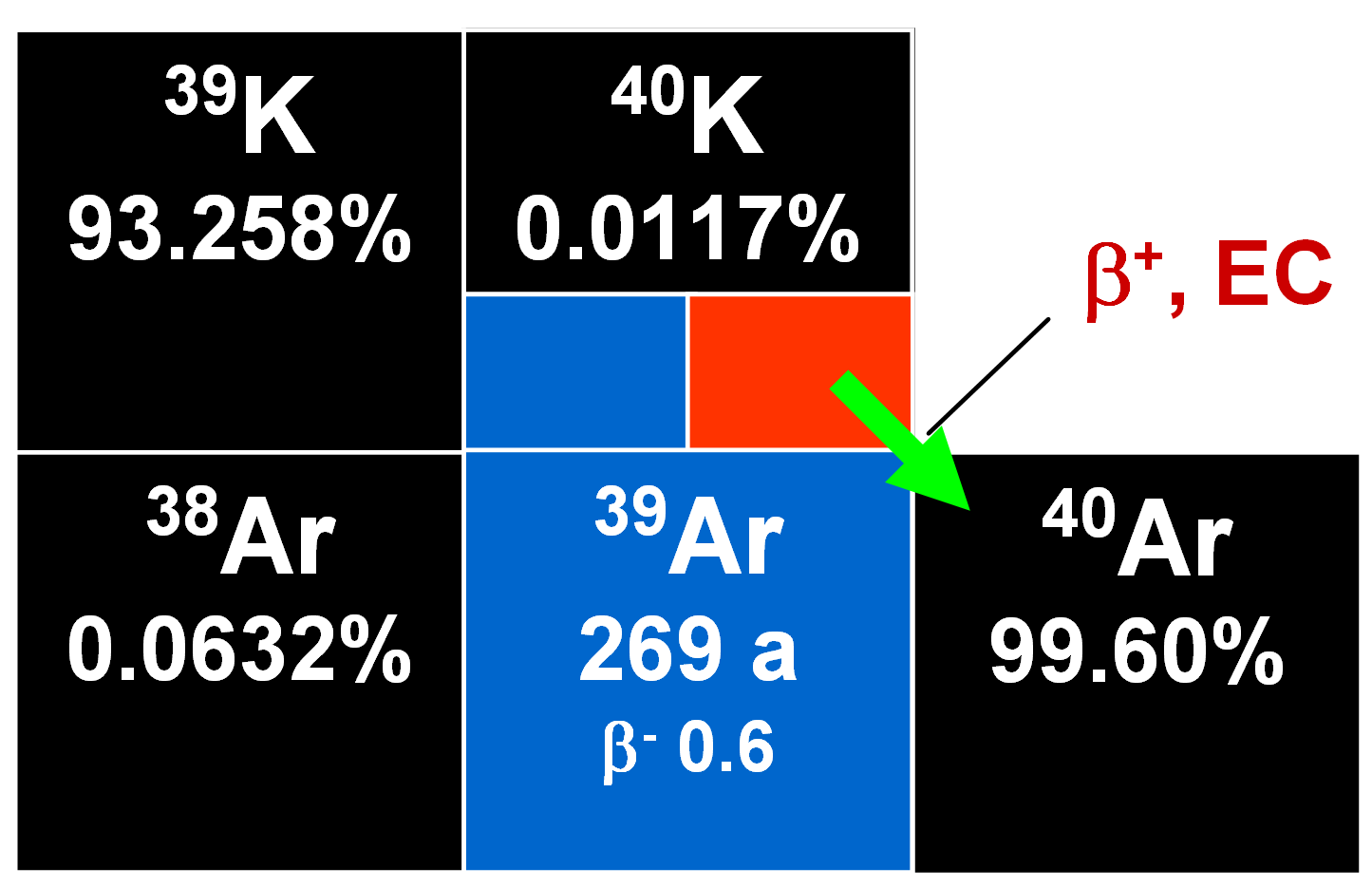
Potassium has one long-lived naturally occurring radioactive isotope 40K with a half-life of 1.28•109 y. It undergoes branched radioactive decay to 40Ca and 40Ar. This leads to the fact that the abundance of 40Ar in the atmosphere is orders of magnitude higher than would be expected by comparison with abundances of the other noble gases. Hence excess 40K should also occur in ancient potassium-containing minerals. Once this was found to be the case, the foundation of the K/Ar dating method was laid. The natural relative abundances of 40K and 40Ar are 0.0117% and 99.600 %, respectively.

11% of the 40K decay by electron capture (EC) to an excited state of 40Ar that de-excites by emitting a gamma ray with the energy of 1462 keV. About 0.16% of the decays take a more direct route by EC straight to the ground state of 40Ar. Positron (β+) decay is rare with a branching ratio of only about 0.001 % with an Eβmax of 0.49 MeV. It is followed by annihilation radiation of 2 times 511 keV.

The branching ratio for negatron (β-) decay to stable 40K is about 89 %.

In a potassium-bearing system closed to all external influences through geological time, the growth of radiogenic 40Ar and 40Ca can be represented as:



where λK=λEC+λβis the total decay constant of 40K, and all numbers of atoms including that of 40K refer to the same moment t.

Each branch of the decay mode has its own decay constant and these are as follows. For 40K to 40Ar it is λEC=0.581 • 10-10 y-1 and for 40K to 40Ca it is λβ=4.962•10-10 y-1. Summing gives a value for λK of 5.543•10-10 y-1. The branching ratio is, as mentioned before, about 0.11. It should be added that there are other, slightly different, values for the decay constants in the literature.

The growth of radiogenic 40Ar atoms in potassium-bearing minerals is given by




where λEC is the decay constant for the decay of 40K to 40Ar.

The total number of 40Ar atoms will be the sum of the radiogenic ones and any which were present when the mineral formed and became occluded in the forming minerals.

If we assume that no 40Ar was present initially, the 40Ar concentration must have originated from the decay of the present 40K only. If this is the case, the age of the mineral, t, can be derived from:




A few other assumptions have to be made in order to derive values for t from various minerals. One is that none of the radiogenic 40Ar arising from the radioactive decay of 40K in the mineral during its geological history has escaped by diffusion. Another is that the mineral closed off the 40Ar soon after crystallization, hence rapid cooling must have occurred.

It is implicit in the method that no excess 40Ar became incorporated in the mineral when it crystallized or during any subsequent metamorphic episodes. Finally, it is assumed that the mineral remained closed to potassium throughout its geological history so that the isotopic composition of the potassium in it must have altered solely through radioactive decay of the 40K originally present and no isotopic fractionation took place. A correction is necessary for the presence of atmospheric 40Ar. Also, the potentially disturbing effects of argon being over-pressurized in extremely old basement rocks have to be considered because the gas might be released during metamorphism (Roddick 1983). However, it has been claimed that this may not always happen (Dempster 1986).

If argon loss occurred in a mineral, it happened usually because of metamorphism, this phenomenon showing the inability of argon to bond with other atoms in a crystal lattice. In fact, minerals have difficulty in retaining the gas even at quite low temperatures and at atmospheric pressure. So it is not surprising that the concept of closure temperatures below which, when minerals formed, crystallization ages were recorded, has been increasingly criticized. In the western Alps and Norway, old ages were retained despite later metamorphic temperatures believed to have exceeded the supposed closure temperatures (Chopin and Maluski 1980, Verschure et al. 1980). Clearly, other factors such as chemical weathering, deformation, ex-solution and recrystallization may affect mineral age relationships. Naturally, only potassium-bearing minerals, rocks and minerals able to resist as many as possible of these adverse influences are appropriate for dating by the K/ Ar method. In fact, such rocks and minerals are quite common. Basaltic glass can retain argon well, but hydrated glass cannot, especially if de-vitrified.

Excess radiogenic 40K may occur in some potassium-bearing minerals and its effects on K/Ar ages are most marked in young minerals or those with low potassium content. However, while beryl, cordierite and tourmaline often contain such excess radiogenic 40Ar, other minerals do not. The excess gas can result from the relevant minerals having been exposed to high partial pressure of the gas during an episode of regional metamorphism when pegmatites crystallize or kimberlite pipes are emplaced. In addition, it may diffuse into minerals as a result of the out-gassing of older potassium-bearing minerals in the crust and mantle of the Earth or from older xenoliths or xenocrysts. Whenever it happens, K/Ar ages are increased and therefore give over-estimates for the ages of minerals containing it. Minerals used in such dating have different blocking temperatures, e.g. that of biotite is lower than that of hornblende. So the K/Ar 'clock' of the hornblende starts before that of biotite since cooling is in progress. If temperature decrease was smooth and both minerals constituted closed systems since crystallization, the hornblende will register an older date than the biotite. If two such different dates are obtained, they can be used to infer the cooling rate.