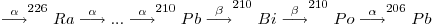
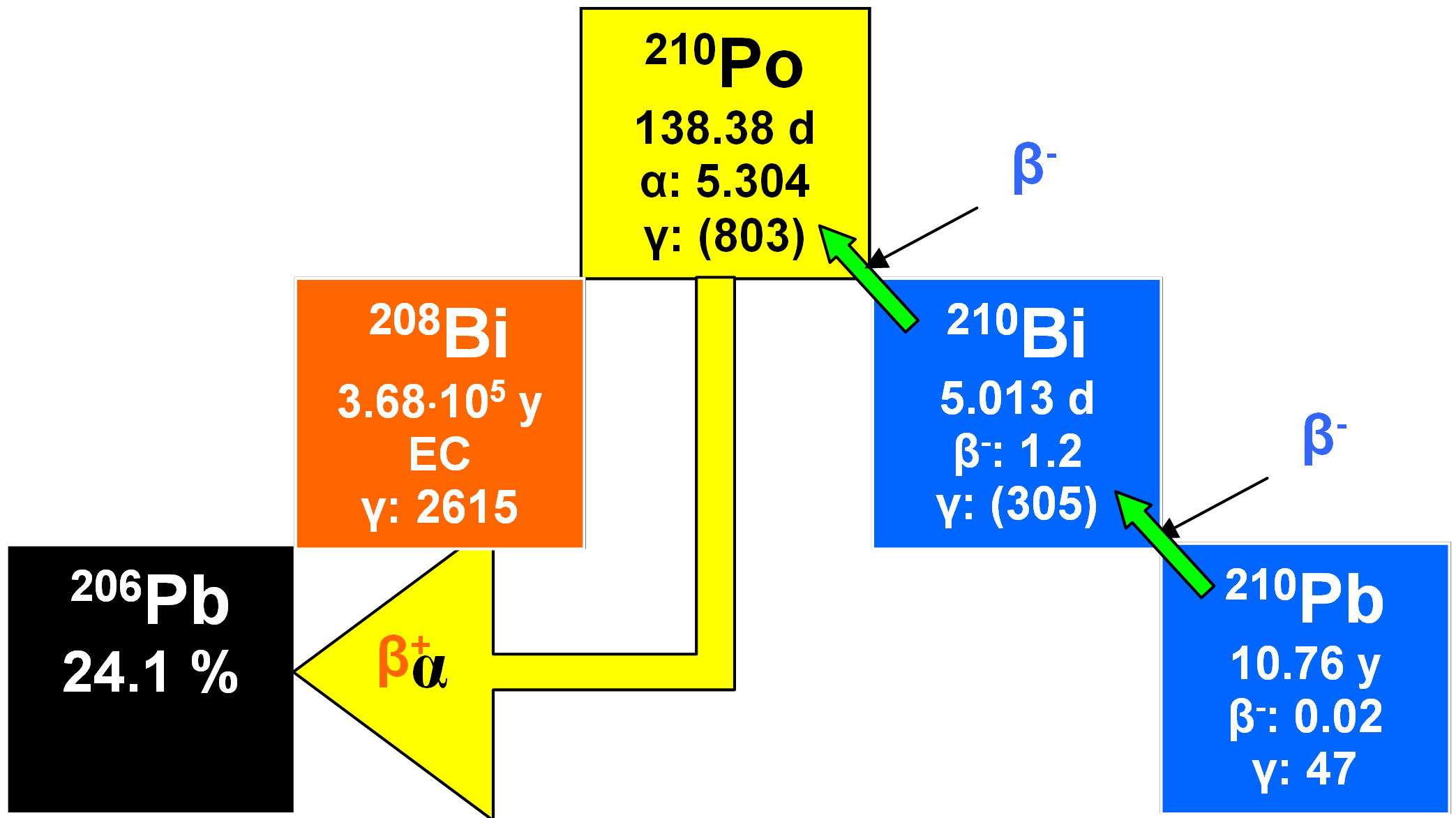
In an undisturbed (closed) system, that is to say one at secular or radioactive equilibrium, 210Po has the same activity as the other radionuclides in this series. Preceded by 210Bi, its immediate parent (half-life 5.013 days), it reaches equilibrium relatively rapidly with its grandparent 210Pb.
The method described briefly here has been suggested to date glassy eruption products within a few years after eruption (Rubin et al. 1994). The method is based on the fact that during eruption de-gassing occurs. This affects not only the obvious noble gas precursor 222Rn, but also 210Po since its compounds (e.g. its halogenides) are rather volatile (even the pure metal has a fairly low boiling point of 962°C). So it is thought to be completely gaseous in volcanic eruptions at about 4000°C. Due to the very short half-lives of the nuclides between 222Rn and 210Pb in the decay series, equilibrium gets re-established again within a few weeks all the way from 226Ra down to 210Pb, so that the activity of the latter can be considered constant before, during and after eruptions.
The calculation is based on a simplified form of the Bateman equation for closed system radioactive decay to describe the 210Po content of de-gassed lavas as a function of time. Using appropriate initial conditions for solving Eq. (36) in Chapter 5, Volume I, we get the following relationship for the activities:
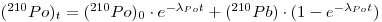
where λPo is the decay constant of 210Po and t is the time elapsed since the eruption.
For the numbers of atoms we have a slightly more complicated formula involving also the decay constant λPb of 210Pb:
![[^{210}Po]_t=[^{210}Po]_0\cdot e^{-\lambda_{Po}t}+[^{210}Pb]\cdot\frac{\lambda_{Pb}}{\lambda_{Po}}\cdot(1-e^{-\lambda_{Po}t}) [^{210}Po]_t=[^{210}Po]_0\cdot e^{-\lambda_{Po}t}+[^{210}Pb]\cdot\frac{\lambda_{Pb}}{\lambda_{Po}}\cdot(1-e^{-\lambda_{Po}t})](math/309944a36ba654d290551ea628f24777.gif)
To calculate t from one measurement of (210Po), it is necessary to know both (210Pb) and (210Po)0. While for a totally de-gassed lava, the value of the latter parameter would be zero, it is probable that only partial de-gassing may take place in the case of for instance submarine lavas which erupted under high hydrostatic pressure. However, it is feasible to calculate a unique maximum value to t by assuming that total de-gassing occurred and fitting an exponential function to a set of measurements made on a sample as 210Po grows into equilibrium with 210Pb (Rubin et at. 1994). The maximum age corresponds to (210Po)0 = 0 on the best fit growth curve. The approach was applied to East Pacific Rise (EPR) lavas and repeated measurements of (210Po) over several years were made on aliquots of each sample together with in-growth curves having the functional form of the above equation. They were fitted to the data using the time interval between sequential measurements in order to constrain t. The regression results gave a function for (210Po) and the known analysis times linked the results to calendar time.
If de-gassing was not complete at eruption, the eruption time cannot be accurately ascertained, but is bracketed in every case by the 'window' between collection of sample and calculated maximum age. Such 'windows' (eruption dates) are most accurately determinable for samples either having the lowest (210Po) when collected or for which the initial (210Po) can be estimated independently. Samples have been obtained from mid-ocean ridge basalts (MORBs) and these have similar chemical compositions and were erupted at the same water depth, both factors possibly affecting the efficiency of de-gassing. Hence, it can be anticipated that all will have more or less the same initial (210Po)0. But the de-gassing content may not be as high as the sub-aerial value of 100%. Two samples were analyzed by Rubin et at. (1994) and had the same 210Po contents at the time of collection which were only about 25% of the secular equilibrium value (25.1% and 25.6%, respectively) implying that all samples were minimally 75% de-gassed in the course of the eruption.