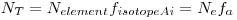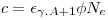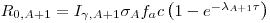Back to Main

We have:
A_0=\sigma\phi N_T\left(1-e^{-\lambda\tau}\right)
 (1)
R_0=I_{\gamma}\epsilon_{\gamma}A_0
 (2)
Here σ is the cross section of the reaction with thermal neutrons, φ is the flux of the neutrons, NT is the total number of atoms in the sample, I𝜸 is the relative intensity of the 𝜸-ray we are looking at, A0 is the activity of the sample at time zero and R0 is the count rate of the sample at time zero.
If the target contains several isotopes, as silver does, we must take into account the isotope fraction, for each isotope in our target:
N_T=N_{element}f_{isotopeAi}=N_e f_a
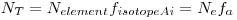
 (3)
Where the right part of the equation shows the abbreviated indexes we are going to use.

E.g. for silver there are two stable isotopes: 107Ag and 109 Ag, with isotope fractions equal to 51.839% and 48.161% respectively. Ne equals the total number of silver atoms in your sample.
So, combining (1),(2) and (3) we end up with:
R_{0,A+1}=I_{\gamma,A+1}\epsilon_{\gamma,A+1}\sigma_{A}\phi N_e f_a \left(1-e^{-\sigma_{A+1}\tau}\right)
 (4)
This formula will calculate the cont rate for isotope A+1 after an irradiation time 𝛕 of stable isotope A. I𝜸 =1.76% for the 633 keV 108Ag
𝜸-ray and 4.5% for the 658 keV 110Ag.

We can relate the count rate for the two silver-isotopes by observing that φ and Ne if course will be equal and that ε𝜸,A+1
for the two 𝜸-rays (at 633 keV and 658 keV, respectively) will be practically equal since the energies are so close. I.e we define a constant:
c=\epsilon_{\gamma.A+1}\phi N_e
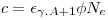
 (5)
which do not depend on the irradiated isotope.Then:
R_{0,A+1}=I_{\gamma,A+1}\sigma_A f_ac\left(1-e^{-\lambda_{A+1}\tau}\right)
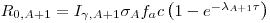
 (6)
We can determine c from e.g the measurement of R0,110 from the 144 s irradiation of 110Ag:
R_{0,110}=I_{\gamma,110}\sigma_{109}c\left(1-e^{-\lambda_{A+1}144}\right)
 (7)
Then theoretical values for R0,108 and R0,110 for any irradiation time can be estimated. In the laboratory exercise you will measure the R0 values for both isotopes for irradiation times 𝛕 =12,24,48,72 and 144 s. Thus, by using the value from (7) you can estimate the values for the nine (9) other cases and compare them to the measurement values.