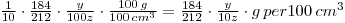- Take two 2 cm3 aliquots of 35S-spiked strontium nitrate solution and place in separate 15 ml centrifuge tubes, add excess 2.5 M sulphuric acid (approx. 4-5 cm3) – a white precipitate will rapidly form
- Centrifuge at 5000 rpm for 5 min and then pour off supernatant into the waste beaker provided
- Wash repeatedly with distilled water using at least 100 cm3 – carefully pour off wash water into the waste beaker leaving the precipitate in the centrifuge tube each time
- Add 10 cm3 of distilled water to the washed precipitate and leave to stand for 10-30 min, shaking periodically – this allows time for precipitate and water to equilibrate (see step 9)
- Meanwhile dilute the strontium nitrate solution by a factor of 100 in the volumetric flask with distilled water– use 0.25 cm3 in 25 cm3
- Add 10 cm3 of scintillation fluid to 5 plastic scintillation vials
- Add 1 cm3 of original undiluted solution to the1st vial
- Add 1 ml of the 100x diluted solution to a 2nd vial
- Once the strontium sulphate has equilibrated, centrifuge off the precipitate and add 1 cm3 of the supernatant from 1st precipitated sample to a 3rd vial
- Add 1 cm3 of the supernatant from the 2nd precipitated sample to a 4th vial
- The 5th vial has no activity added and is the background sample
- Count all 5 vials on liquid scintillation counter using 14C channel (Protocol 2). Press button F2 to start the run.
As the majority of the activity is in the precipitate, it is clear that a minute amount of this in the supernatant may cause a gross error in the determination.
From the results obtained the solubility of strontium sulphate may be determined as follows:
Let count of 1 cm3 original solution diluted 1/100th=z cpm
Let count of 1 cm3 of SrSO4 = y cpm
Thus, 100z cpm is equivalent to 0.1 g Sr(NO3)2
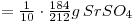
y cpm is equivalent to:
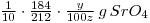
Solution of SrSO4=