The pulse spectra are obtained by passing the output pulses from the detector through an amplifier to a multichannel analyser. The multichannel analyser stores and displays the pulse as a histogram of number of pulses versus channel number, the channel number representing a narrow range of pulse sizes. NaI(Tl) scintillation detectors are reasonably efficient in detecting γ-radiation, but have poorer energy resolution than semi-conductor devices.
Part 1 - Energy Calibration Using 4 Known Isotopes
- Put the 137Cs source on the top of the detector and obtain the spectrum by pressing F1
- Stop acquiring it (press F1 again) when the peak gets near the top of the screen. The peak height can be scaled by using the up or down arrows followed by enter, if you want to make it bigger or smaller
- Record the channel number for the photopeak by moving the cursor using the side-to-side arrows until it is at the peak
- From the 137Cs peak, identify the channel numbers for the Compton Edge and the backscatter peak
- Replace the 137Cs source with the 60Co and record the channel numbers for the 2 photopeaks
- Repeat with the 22Na source
- Draw a rough graph of the channel number (x-axis) against photopeak energy. It should be a straight line passing through the origin
- Repeat with the 133Ba source and identify as many of the five photopeaks as you can (probably 3 or 4). Remember that the peaks must fit on the straight line, as there is a danger of misidentification of peaks with this isotope.
- Include this graph (drawn on Excel) in your write-up.
- Record the trend line formula and R2 value.
Part 2 - Identifying the Unknowns
- Record the spectrum for the first unknown isotope (in the small plastic pot) and determine its 3 photopeak energies using your channel number-energy calibration curve.
- Identify the isotope using the gamma-ray energy tables provided here.
- The second unknown is a sample of Icelandic moss. In this you should find 2 separate single peak γ-photon emitting isotopes. One is from a naturally occurring element, and the other is from fallout from the Chernobyl nuclear accident in 1986. Identify these two radioisotopes using the gamma-ray energy table provided here.
- The third unknown is a soil sample from the edge of Glubokye Lake a few kilometres from the Chernobyl reactor site. It is known the nuclear fuel particles are present here. Can you find any evidence of actinide elements present in this sample? Ignore the 137Cs peak and look at the low energy end of the spectrum in the following way.
- Obtain the spectrum and move the cursor to channel number 1 while it is growing
- Stop acquiring the spectrum.
- Use F4 and the down arrow followed by ‘enter’ to set the ‘x’ scale to 128.
- The large peak at channel number 20 (ish) are caused by the 137Ba X-rays, ignore it. Now working from low channel to high channel identify any peaks you can find, from the actinides only table (located towards the bottom of this page). Stop when you reach the 137Cs peak. Take into account the half-life and the gamma yield of the isotopes.
Part 3 - Determination of Energy Resolution Using Cs-137
Whether two peaks close to each other can be resolved or not depends on two factors, the efficiency of the spectrometer, and the statistical spread of the peaks. The spread of the peak is due to statistical variation in the scintillations, and in the performance of the photomultiplier. The crystal must be clear and give large cintillations. These must be registered efficiently by the photocathode and the photoelectrons produced must be efficiently collected at the first dynode. This collection is sometimes improved by doubling the voltage across the first stage. The resolution should be much lower (i.e. superior) for semi-conductor detectors.
1. Measure the photopeak width for 137Cs at 1/2 max height, using channel numbers (channel number halfway up on the right - channel number halfway up on the left)
2. Re-determine the channel number of the photopeak.
3. The resolution obtainable by a particular spectrometer is given by:
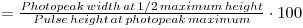
4. This should give a value of about 10% or less for the NaI(Tl) scintillation detector