Back to Measurements, uncertainty and Detection Limits

Evaluation of Type A Uncertainty

Let Xi be an input quantity in the mathematical model for Y. A series of n independent measurements of Xi are made under the same experimental conditions, yielding the results Xi,1, Xi,2, …Xi,n. The appropriate value for the input estimate xi is the arithmetric mean defined as: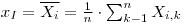
x_I=\overline{X_i}=\frac{1}{n}\cdot\sum^{n}_{k-1}X_{i,k}
 Eqn. 1

The experimental variance of the observed values is defined as:

S^2(X_{i,k})=\frac{1}{n-1}\cdot\sum^{n}_{k-1}\left(X^2_{i,k}-\overline{X_i}\right)^2
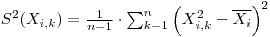 Eqn. 2


The experimental standard deviation, s(Xi,k), is the square root of s2(Xi,k). The experimental standard deviation of the mean is defined by:

u(X_i)=\sqrt{\frac{1}{\cdot(n-1)}\cdot\sum^{n}_{k-1}\left(X_{i,k}-\overline{X_i}\right)^2}
 Eqn. 3

Example:
10 independent measurements of a quantity Xi are made yielding the values:

15.235
 15.333
 15.458
 15.641
 15.124
15.280
 15.701
 15.427
 15.222
 15.564

From Eqn. 1 above on determines that

x_i=\overline{X_i}=\frac{153.985}{10}=\underline{15.3985}
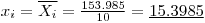
The standar uncertanity of Xi is:

u(x_i) = s(\overline{X_i})=\sqrt{\frac{1}{10\cdot(10-1)}\cdot\sum^{10}_{k-1}((X_{i,k}-15.3985)^2}=0.061
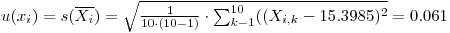
and the masured number would be denoted
\underline{\overline{X_i}=15.399\pm0.061}
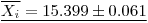
or, when considering the uncertainty in he uncertainty, rather
\underline{\overline{X_i}=15.40\pm0.06}

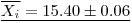
Evaluation of Type B Uncertainty

One example of a Type B method is the estimation of counting uncertainty using the square root of the observed counts. If the observed counts is S, when the Poisson counting model is used, the standard uncertainty of S may be evaluated as: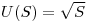

U(S)=\sqrt{S}
 Eqn. 4
Sometimes a Type B evaluation of u(x) consists of estimating an upper limit a to the error based on professional judgement of best available information. If the error has a uniform distribution, u(x) may be calculated by:
u(x)=\frac{a}{\sqrt{3}}
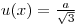 Eqn. 5