A common question arises in low-level radioactivity measurements: Is the signal there? What is the chance that we will detect it? How big is it?
There has been much inconsistency in definition of “detection limit”. The various definitions historically used spans a factor of nearly 1000.
The turning point, or rather focusing point came with a publication by Currie in 1968 ^[1] . On the basis of statistical hypothesis testing he defines three limiting levels:
LC, the critical level which is the signal level above which an observed instrument response may be reliably recognized as “detected”
LD, the detection limit which is the true net signal level that may be expected a priori to lead to detection
LQ, the determination limit which is the signal level above which a quantitative measurement can be performed with a stated relative standard deviation.

A few Relevant Definitions

The “null” hypothesis H0 – The analyte concentrations of the material is no greater than that of the blank
The “alternative” hypothesis H1 – the analyte concentration of the material is greater than that of the blank
False positive - Type I decision error- the error made by rejecting the null hypothesis when it is true – often denoted by the parameter α with a value of 0.05
False negative – Type II error – the error made by failing to reject the null hypothesis when it is false – often denoted by β with a value of 0.05

The Critical Value of Response Variable

Definition

In an analyte detection decision one chooses between the “null” and the “alternative” hypothesis on the basis of the observed response variable Y. The value of Y must exceed a certain threshold to justify the rejection of the null hypothesis. This threshold is called the critical value of the response variable and denoted by yC (or LC).
Calculation of yC requires the choice of a significance level for the test. This is a specified upper limit for the probability,α, of a Type-I error (false rejection). The significance level is often chosen to be 0.05. This means: When an analyte-free sample is analysed, there should be at most 5% probability of incorrectly deciding that the analyte is present.

Decision Level Concentration

The critical value of the analyte concentration xC (or SC), also called decision level concentration DLC, is the value obtained by applying the evaluation function F-1 to yC:

$S_c=F^{-1}(y_c)$

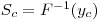eqn 1

This formula typically involves division by the counting efficiency, test portion size, chemical yield, decay factor and possibly other factors.
The critical value of the net signal SC is defined symbolically by:

$Pr[\hat{S}>S_c \| X=0] = \alpha$

eqn 2

denoting the probability that the observed signal Ŝ exceeds its critical value SC when the true analyte concentration X=0 and a denotes the significance level or the specified probability of Type-I error.

Derivation of SC - Formulas

If the distribution of the net signal Ŝ under Ho is approximately normal with a well-known standard deviation s0, the critical value of Ŝ is simply:

$S_C=Z_{1-\alpha}((0$

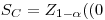eqn 3

where z1-α denotes the (1-α)-quantile of the standard normal distribution. Here, z1-α ≈ 1.645 when α = 0.05.

Suppose Poisson-distributed blank, no interference and no non-Poisson blank variance. The critical level is then expressed by:

$S_C=Z_{1-\alpha} \cdot \sqrt{R_B\cdot t_{s}\cdot\left(1+\frac{t_s}{t_b} \right)}$

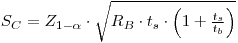eqn 4

where RB is the true mean count rate of the blank, ts is the counting time for the test source and tB is the counting time for the blank.

The preceding formula is equivalent to “Currie’s equation”:

$S_C=2.33\cdot\sqrt{\mu_B}$

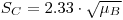eqn 5

when tB

tS, α

0.05, and the symbols LC and mB are identical with SC and RBtS, respectively.

In practice one must substitute an estimated value ŘB for RB:

$S_C=Z_{1-\alpha} \cdot \sqrt{\check{R}_B\cdot t_s\cdot \left(1+\frac{t_s}{t_B}\right)}$

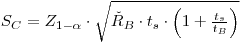eqn 6

The value of ŘB is usually estimated from the same blank value SB used to calculate the net instrument signal:

$\check{R}_B=\frac{S_B}{t_B}$

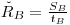eqn 7

Introducing this into the previous formula gives:

$S_C=z_{1-\alpha}\cdot\sqrt{\check{S}_B\cdot\frac{t_s}{t_B}\cdot\left(1+\frac{t_s}{t_B}\right)}$

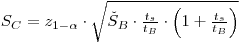eqn 8

Example of Calculating of SC

Problem:
A 2 hours (= 7200 s) blank measurement is performed on a proportional counter and 123 beta counts are recorded. A test source is to be counted for 1 hour (= 3600 s). Estimate the critical value of the net count when α= 0.05.

Solution:
Set in proper values in the preceding formula:

$S_C=1.645\cdot\sqrt{123\cdot\frac{3600}{7200}\cdot\left(1+\frac{3600}{7200}\right)}=15.8 \, net\, counts$

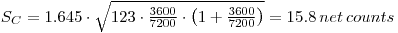
Minimum Detectable Concentration

Definition

The minimum detectable concentration (MDC) is defined as the concentration of analyte xD that must be present in the sample to give a specified probability, 1-β, of obtaining a measured response greater than its critical value, leading one to conclude correctly that there is analyte in the sample. In other words, the MDC is the analyte concentration at which the Type II error rate isβ, or in different wording: The MDC is by definition the true concentration of analyte required to give a specified high probability that the measured response will be greater than the critical value.

The MDC may also be defined as the analyte concentration that satisfies the relation:

$Pr [\check{S} \leq S_C \| X=x_D]=\beta$

eqn 9

which is read as “the probability of the net signal Ŝ does not exceed its value SC when the true concentration X = xD.

Derivation of SD - formulas

For Poisson counting:
If the mean blank count is at least 100, α=β, the only source of signal variance considered is Poisson counting statistics and Eqn. 8 is used to calculate the critical net signal SC:
The minimum detectable net signal SD is given by:

$S_D=z^2_{1-\beta}+2S_C$

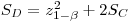eqn 10

In the special case when α= β =0.05, Eqn. 10 becomes:

$S_D=2.71+2S_C$

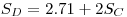eqn 11

3.3.3. Example of calculation of SD

Problem:
A 7200 second blank measurement is performed on a proportional counter and 123 beta counts are recorded. A test source is to be counted for 3600 s. Assume that α=β = 0.05. Calculate the minimum detectable net signal SC:
Solution:
Use Eqn.8 to calculate SC and Eqn.11 to calculate SD. Inset of proper values gives:

$S_D=2.71+2\cdot(15.8)34.3\, counts$

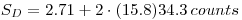
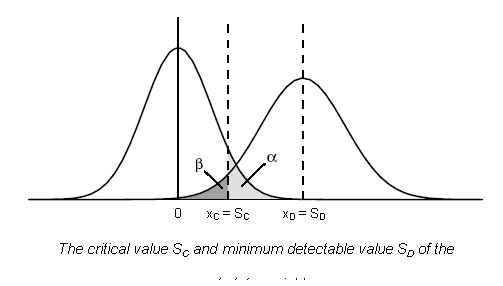
Illustration of the relation between SC and SD is given below:

Minimum Quantifiable Concentration

The minimum quantifiable concentration (MQC) is defined as the analyte concentration in a laboratory sample that gives measured results with a specified relative standard deviation 1/kQ, where k is usually chosen to be 10.
The MQC is defined symbolically as the value xQ that satisfies the relation

$X_q=k_q\cdot\sqrt{\sigma^2(\check{X}\|X=x_q)}$

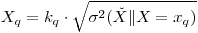eqn 12

where the expression under the square root denotes the variance of the estimator ^X when the true concentration X = xQ. In simple cases xQ is easily calculated by algebraic manipulations. More complicated cases require fixed-point iteration.

^ Lloyd A. Currie: “Limits for Quantitative Detection and Quantitative Determination: Application to Radiochemistry”, Anal. Chem. 40, (1968) 586-593