In this exercise you are to do an efficiency calibration of a Ge-detector. The efficiency to any detector is dependent on quantities such as the γ-rays energy, the geometrical shape and size of the source, and the distance between the source and detector. In order to make an efficiency calibration we use sources with a known amount of activity. The sources are measured and then we can calculate the counting efficiency: If the source activity is A, the number of counts obtained with a given detector is R, then the counting efficiency is given by:
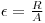
To calibrate a γ detector we must also take into consideration that a γ ray will not necessarily be emitted every time the source disintegrate. The frequency γ rays are emitted can be found in tables and is given as the γ intensity, usually symbolized with Iγ. The formula we use to calculate the efficiency then looks like this:
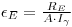
Notice that we have indexed the ε and R with an E to indicate that these are energy dependent. Since all the absorption processes for γ radiation is strongly dependent on the γ-ray energy, the detector efficiency will also be dependent on energy. Thus, to calibrate a γ detector we must use a range of sources with energies that cover the range of energy we are planing to measure in. The efficiency calibration will then look like something in Fig 1. The most common range to measure γ radiation in is from about 50 keV and up to about 1-2 MeV. From Figure 1 we can see that the range between about 200 keV and up to 2 MeV is nearly linear in double-logarithmic scale. Below 200-250 keV this is not true.
 |
|---|
| Fig 1: Detector efficiency for two types of Ge-detector. notice that the plot is on a double logarithmic scale. |
In this exercise we have measured a series of standard γ-ray sources with a HPGe-detector (High Purity Germanium Detector)